Теплоход в движении был 13-3=10 часов.
Скорость теплохода по течению равна 20+4=24км/ч.
Скорость теплохода против течения равна 20-4=16 км/ч.
Пусть по течению теплоход шел х часов, а против течения - у часов. Зная, что всего в движении он был 10 часов, составляем первое уравнение:
х+у=10
По течению теплоход х км, против течения - 16у. Зная, что оба расстояния равны, составляем второе уравнение:
24х=16у.
Получили систему уравнений:
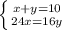 ⇒
⇒ 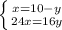
24(10-у) = 16у
24у + 16у = 240
у = 6
х = 10-6 = 4
Теплоход по течению плыл 4 часа, а это 24·4 = 96 (км)
За весь рейс теплоход км)
ответ. 192 км.
1. Нам нужно найти знаменатель q, который должен быть отрицательным, т.к. прогрессия знакочередующаяся.
Выражаем третий и пятый члены прогрессии через ее первый член и знаменатель: b3 = 3q²; b₅ = 3q⁴.
Зная, что их сумма равна 60, составляем уравнение:
3q²+3q⁴=60
3q⁴+3q²-60=0 /3
q⁴+q²-20=0 - биквадратное уравнение
q²=t
t²+t-20=0
По теореме Виета: t₁ = -5 - не подходит, т.к. q²≠ -5
t₂ = 4 ⇒ q²=4
Нас интересует только отрицательный корень. q=-2
2. Находим b₂.
b₂ = b₁ q
b₂ = 3·(-2) = -6
ответ. -6
при х = 18 ответ 818, при х = 27 ответ 827
2) 239 + ( y + 11 ) = ( 239 + 11 ) + y = 250 + y
при y = 53 ответ 303, при у = 65 ответ 315
3) ( 442 + х ) + 58 = ( 442 + 58 ) + х = 500 + х
при х = 29 ответ 529, при х = 34 ответ 534
4) ( 563 + у ) + 37 = ( 563 + 37 ) + у = 600 + у
при у = 16 ответ 616, при у = 72 ответ 672
5) ( 316 + х ) + 84 = ( 316 + 84 ) + х = 400 + х
при х = 14 ответ 414, при х = 30 ответ 430
6) 637 + ( у + 63 ) = ( 637 + 63 ) + у = 700 + у
при у = 15 ответ 715, при у = 26 ответ 726