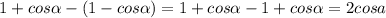Пошаговое объяснение:
Идея решения состоит в том, чтобы умножить числитель и знаменатель на сопряженное знаменателю выражение (то есть, чтобы в знаменателе получилась разность квадратов):
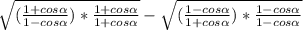
В числителе находится выражение, стоящее под корнем и возведенное в квадрат. Значит, оно равно этому выражению, стоящему под модулю, то есть:
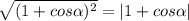
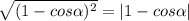
Знаменатель - следствие из основного тригонометрического тождества. В результате получается следующее:
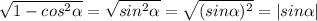
Модуль, полученный в числителе, можно убрать, т.к. min значение не меньше 0.
Т.к. знаменатели обеих дробей равны, то можно из первого числителя вычесть второй: