Пошаговое объяснение:
7. Центральный угол на 35 градусов больше вписанного угла, опирающегося на ту же дугу. Найдите каждый из этих углов .
------------------
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
х градусов - вписанный угол. Тогда центральный угол равен 2х градусов.
2х-х=35°;
x=35° - вписанный угол.
х+35° =35°+35°=70° - центральный угол.
------------------
8. найдите вписанный угол, опирающийся на дугу, составляющую 1/8 окружности.
---------
Градусная мера окружности равна 360°. Тогда
1/8 часть окружности равна 360/8=45°.
Вписанный угол равен половине дуги, на которую он опирается=> 45/2=22.5°.
--------
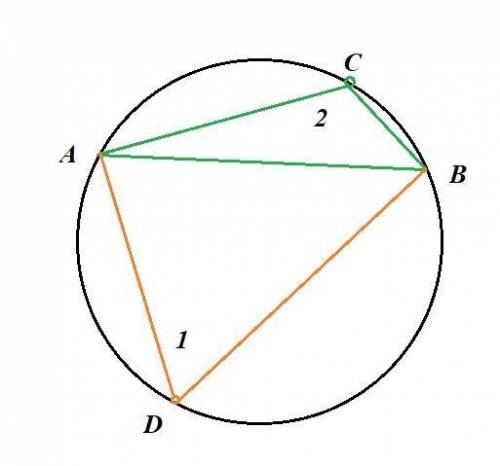
10. хорда делит окружность на две дуги , относящиеся как 2:7 . Под каким углом видна эта хорда из точек окружности?
------------
Градусная мера окружности равна 360°. Тогда
1 дуга равна 2х градусов и 2 дуга равна 7х градусов
2х+7х=360;
9х=360;
x=40°.
1 дуга равна 2х=2*40°=80°.
2 дуга равна 7х=7*40°=280°.
Угол, вершина которого расположена на окружности называется вписанным и равен половине дуги на которую он опирается.
Угол 1 равен 80°/2=40°.
Угол 2 равен 280°/2=140°.
См. скриншот.
48 см
Пошаговое объяснение:
Так как сумма соседних углов ромба = 180, то угол BAD = 60.
Так как угол BAK = 60, а угол BKA = 90, то угол ABK = 180 - 90 - 60 = 30.
В прямоугольном треугольнике катет лежащий против угла 30 градусов в 2 раза меньше гипотенузы, то есть AB = 2AK = 16 см.
Так как у нас ромб, то все стороны равны, значит AD = 16 см.
Так как AD = AK + KD, то KD = AD - AK = 16-8 = 8 см
Треугольники ABK и BKD равны по 2 сторонам и углу между ними (AK = KD, BK - общая сторона, угол между соответствующими сторонами 90). Тогда BD = AB = 16 см.
Периметр треугольника ABD = AB+BD+AD = 16+16+16 = 48 см