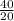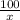
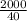
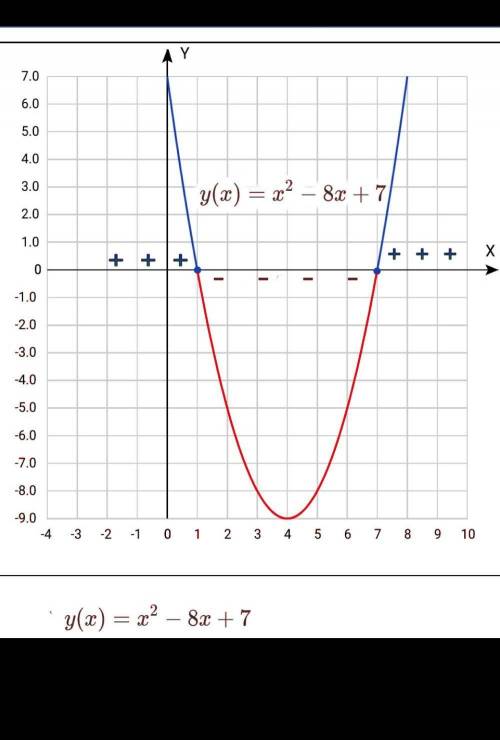
= 
См рисунок
и
![x \in \: (- \infty ; \: 1] \: \cup \: [7; \: + \infty )](/tpl/images/1853/9951/0b25b.png)
Пошаговое объяснение:
1) Построим график функции.
Графиком функции является парабола, ветви вверх.
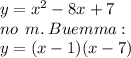
Парабола пересекает Ох в точках (1; 0) и (7; 0)
График приведен на рисунке.
По поводу неравенства:
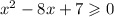
Неравенство нестрогое - поэтому граничные точки включаются в решение. На графике видно, что неравенству удовлетворяют те части параболы, которые находятся НАД осью Ох. Включая и сами точки, в которых значенте функции равно нулю.
На рисунке часть графика НЕ удовлетворяющая неравенству обозначена красным.
Синий цвет графика - решение неравенства. Как видно, это 2 промежутка:
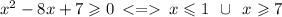
или же:
