7(2x+9)+3x=114. решите с решением и сравнением(например: решение - 144=114) заранее

👇

Увидеть ответ

Ответ:

помагите71

17.03.2022

7(2х+9)+3х=114 14х+63+3х=114 17х=114-63 17х=51 х=51:17 х=3

4,7(10 оценок)

Открыть все ответы

Ответ:

DashaБорьщ17

17.03.2022

ответ:

При упрощении выражения мы получаем -а⁻⁴, либо же - (1/а⁴).

Пошаговое объяснение: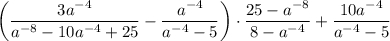

$\displaystyle\bigg( \frac{3a^{-4}}{a^{-8}-10a^{-4}+25}-\frac{a^{-4}}{a^{-4}-5} \bigg)\cdot \frac{25-a^{-8}}{8-a^{-4}}+\frac{10a^{-4}}{a^{-4}-5}$

Введём замену а⁻⁴ = х. Подставляем:

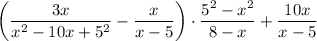
$\displaystyle \bigg( \frac{3x}{x^2-10x+5^2}- \frac{x}{x-5} \bigg)\cdot\frac{5^2-x^2}{8-x} +\frac{10x}{x-5}$

В знаменателе первой дроби мы видим полный квадрат (х-5)² = х² - 2*5*х + 5² (по формуле квадрата суммы (а+b)²=a²+2ab+b²). Записываем знаменатель первой дроби в виде полного квадрата и вторую дробь приводим к этому знаменателю.

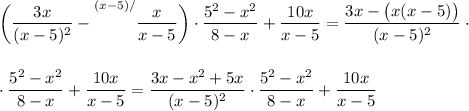
$\displaystyle \bigg( \frac{3x}{(x-5)^2}- {\overset{(x-5)/}{\big{}}}\frac{x}{x-5} \bigg)\cdot\frac{5^2-x^2}{8-x} +\frac{10x}{x-5} = \frac{3x-\big(x(x-5)\big)}{(x-5)^2} \cdot \cdot\frac{5^2-x^2}{8-x} +\frac{10x}{x-5} = \frac{3x-x^2+5x}{(x-5)^2} \cdot\frac{5^2-x^2}{8-x} +\frac{10x}{x-5}$

В числителе первой дроби приводим подобные слагаемые; в числителе второй дроби выносим минус за скобки.

$\displaystyle \frac{8x-x^2}{(x-5)^2} \cdot\frac{-(x^2-5^2)}{8-x} +\frac{10x}{x-5}$

Выносим х за скобки в первой дроби и сокращаем.

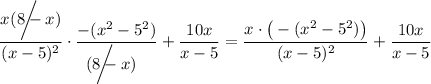
$\displaystyle \frac{x~~ \bigg \slash \!\!\!\!\!\!\!\!\!\!(8-x)}{(x-5)^2} \cdot\frac{-(x^2-5^2)}{\bigg \slash \!\!\!\!\!\!\!\!\!\!(8-x)} +\frac{10x}{x-5}= \frac{x\cdot \big(-(x^2-5^2)\big)}{(x-5)^2} +\frac{10x}{x-5}$

Раскрываем первые скобки в числителе первой дроби и расписываем x²-5² по формуле a²-b²=(a-b)(a+b).

$\displaystyle \frac{-x\cdot~~ \bigg \slash \!\!\!\!\!\!\!\!\!\!(x-5)(x+5)}{(x-5)^{\not2}} +\frac{10x}{x-5} = \frac{-x(x+5)}{x-5} +\frac{10x}{x-5}$

Записываем под общим знаменателем и раскрываем скобки.

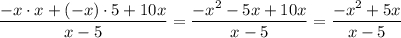
$\displaystyle \frac{-x\cdot x+(-x)\cdot5+10x}{x-5} =\frac{-x^2-5x+10x}{x-5} =\frac{-x^2+5x}{x-5}$

Выносим (-х) в числителе дроби за скобки.

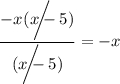
$\displaystyle \frac{-x~~ \bigg \slash \!\!\!\!\!\!\!\!\!\!(x-5)}{~~ \bigg \slash \!\!\!\!\!\!\!\!\!\!(x-5)} = -x$

Возвращаемся к замене а⁻⁴ = х.

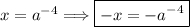
$x = a^{-4} \Longrightarrow \boxed{ -x=-a^{-4}}$

4,6(29 оценок)

Ответ:

rusrusik

17.03.2022

значение производной функции

y=((4x+6)^4)*(x-3) в точке х=-1,5 равно 0

Пошаговое объяснение:

Рассмотрим два случая

В первом условие задачи выглядит так

$y = (4x+6)^4 \cdot (x-3) ~~ ; ~~ x _0 = -1,5$

Во втором

$y = (4x+6)^{4(x-3)} ~ ; ~ x_0 = - 1,5$

В первом случае

$y = (4x+6)^4 \cdot (x-3) ~~ ; ~~ x _0 = -1,5$

Вспомним что :

$\bullet ~ ~(u \cdot v )' = u'v + uv' \bullet ~~ f(g(x)) = f'(g(x))\cdot g'(x)$

Находим производную :

$y ' = ((4x+6)^4 \cdot (x-3)) = ((4x+6)^4)'\cdot (x-3) + (4x+6)^4\cdot (x-3)' y '= (4x+6)'\cdot 4(4x+6)^3\cdot (x-3) + (4x+6)^4 y ' = (x-3)\cdot 8x\cdot (4x+6)^3 + (4x+6)^4 y' = (4x+6)^3 (8x^2 -24x )+(4x+6)^4$

Теперь находим производную в точке x = -1,5

$y'(-1,5) =\underbrace{\Big (4 \cdot (-1,5) + 6 \Big) }_0 \cdot \Big (8 (-1,5)^2 - 24\cdot1,5 \Big)+\underbrace{\Big (4 \cdot (-1,5) + 6 \Big)^4 }_0 = 0$

Во втором случае

$y = (4x+6)^{4(x-3)} ~ ; ~ x_0 = - 1,5$

$y = (4x+6)^{4(x-3)} = \left (e^{\ln(4x+6)} \right)^{4x-12} = e^{\ln (4x+6)\cdot (4x-12)}$

Теперь находим производную используя правила :

$\bullet ~~ (e^{u} ' ) = u ' \cdot e^{u} \bullet ~ ~(u \cdot v )' = u'v + uv' \bullet ~(\ln x ) ' = \dfrac{1}{x}$

$y '= \left (e^{\ln (4x+6)\cdot(4x-12)}\right)' = e^{\ln (4x+6 )\cdot (4x-12)}\right \cdot \Big(\ln(4x+6) \cdot (4x-12)\Big)' y ' = (4x+6)^{4x-12}\cdot \bigg(\dfrac{1}{4x+6}\cdot (4x-12)+ 4\ln(4x+6) \bigg )$

При подстановке x = -1,5

Знаменатель $\dfrac{1}{4x+6}$ равен нулю , а значит условие в данном случае некорректное , и условие должно быть как в первом случае , и ответ на задачу 0