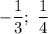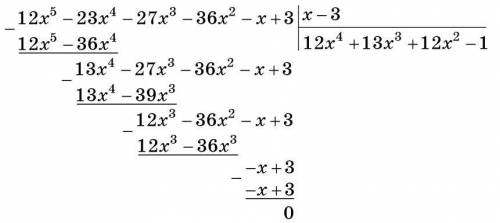Борын-борын заманда булган икән, ди, бер кеше. Бу кеше нең исеме Нарый булган, ди.
Көннәрдән беркөнне Нарый чыгып киткән, ди, юлга. Бара да бара, ди, бу. Бара торгач барып кергән, ди, бу ялтырап торган боз өстенә. Боз өстенә барып керүе булган, аягы таеп, әйләнеп төшүе булган.
— Боз, син нидән болай көчле?
— Көчле булсам,— ди Боз,— мине Кояш эретә алмас иде, — ди.
— Кояш, син нидән көчле? — ди Нарый.
— Көчле булсам, мине Болыт капламас иде.
— Болыт, син нидән көчле?
— Көчле булсам, мине Яңгыр тишеп чыкмас иде.
— Яңгыр, син нидән көчле?
— Көчле булсам,— ди Яңгыр,— мине Җир сеңдермәс иде.
— Җир, син нидән көчле?
— Көчле булсам, мине Үлән тишеп чыкмас иде.
— Үлән, син нидән көчле?
— Көчле булсам, мине Сыер ашамас иде.
— Сыер, син нидән көчле?
— Көчле булсам, мине Пычак кисмәс иде. Хәзер Пычактан сорый инде Нарый:
— Пычак, син нидән көчле?
— Көчле булсам, мине Ут эретмәс иде.
— Ут, син нидән көчле?
— Көчле булсам, мине Су сүндермәс иде.
— Су, син нидән көчле?
— Көчле булсам, мине кеше җиңмәс иде, ә ул мине җиңә, тегермәннәр әйләндерергә җигә! — ди Су.
Шуннан соң Нарый, кешедән дә көчле нәрсә юк икән дип, үз юлына китә, шуның белән әкият тә бетә.
Имеем многочлен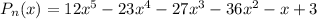 
Корнями многочлена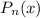 
называют корни уравнения
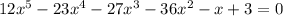
Имеем уравнение пятого порядка. Попробуем его решить с теоремы Безу.
Суть этой теоремы в том, что если уравнение вида с ненулевым свободным членом имеет некий корень , принадлежащий к множеству целых чисел, то этот корень будет делителем свободного члена.
Выпишем все делители свободного члена: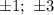 
Подставим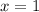 
в корень уравнения и получим:
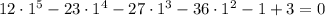
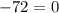— неправда
Подставим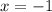 
в корень уравнения и получим:
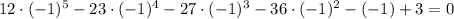
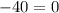— неправда
Подставим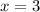 
в корень уравнения и получим:
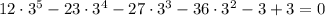
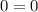— правда
Следовательно,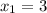 
— один из корней уравнения. Теперь необходимо выполнить деление многочлена столбиком на 
(см. вложение).
После этого исходное уравнение можно записать разложив на множители:
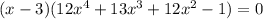
Решаем второе уравнение:
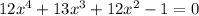
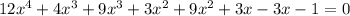
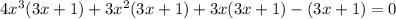
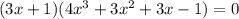
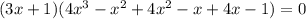
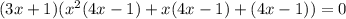
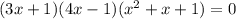
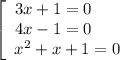
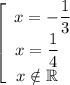
Рациональные корни: 
