Саму задачу можно переформулировать немного по-другому:
Было: Расставить минимальное количество шашек на шахматной доске 8 на 8, так чтобы было невозможно поставить коня так, чтобы он не бил ни одной шашки.Переходит в: расставить на доске минимальное количество коней так, чтобы было невозможно поставить шашку не под удар коня.Если мы решим вторую задачу, то просто нужно будет заменить коней шашками - и мы получим искомое расположение.
По поводу второй задачи можно заметить, что:
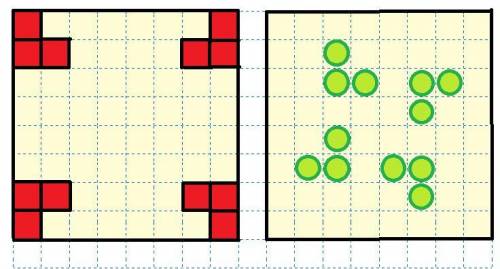
Разные кони должны бить выделенные красным клетки на рисунке ниже.Отсюда следует, что мы не можем расставить менее, чем 4 * 3 = 12 коней. Если это можно сделать, то задача решится. И да, это получилось сделать (рисунок 2).
Заменяем коней шашками и получаем ответ: 12 коней.
ответ: 12 шашек.
66 = 2*33 = 2*3*11
234*798. Умножим только единицы: 4*8 = 40. 40 делится на 5.
Это число иммет вид x*8+5. Подставляете любой x и получаете число. Например, 1*8+5 = 13.
Для того, чтобы число не делилось на 3 нужно, чтобы сумма его цифр не делилась на 3. Например, 123 - 1+2+3 = 6 - делится на 3, 125 - 1+2+5 = 8 - не делится на 3. Для того, чтобы при делении на 5 число давало остаток 2, нужно, чтобы количество единиц было 2 или 7. То есть, мы ищем трёхзначное число вида xy2 или xy7, причем x+y+2 и x+y+7 не делится на 3.
102: делится на 3
107: 107/3 = 35 ост 2, 107/5 = 21 ост 2.
Таким же образом можно подобрать несколько таких чисел.
d1/d2=3/4
4d1=3d2, Постройте ромб и увидите, что он состоит из 4 прямоугольных треугольников, рассмотрим один из них. Один катет будет являтся (d1:2), тогда другой (d2:2).
Выразим d1 по т. Пифагора d1:2=√(a²-(d2/2)²)
Соответственно d1=2√(a²-(d2/2)²)
Подставим, 4*2√(a²-d2²/4)=3d2
8√(a²-d2²/4)=3d2
Возведем обе части в квадрат
64(a²-d2²/4)=9d2²
64a²-16d2²=9d2²
64a²=25d2²
Подставим а=1,5, тогда 64*2.25=25d2²
144=25d2²
d2²=144/25
d2=+- 12/5
d2=+-2.4
d2=2.4, тогда d1=(3*2.4)/4=1.8
ответ: 2.4 ; 1.8.
Надеюсь все понятно и правильно.