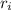 строка
строка  данной матрицы, содержащая ненулевой элемент, и пусть
данной матрицы, содержащая ненулевой элемент, и пусть 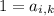 .
.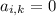 , то
, то 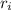 равны нулю,
равны нулю, 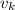 равны нулю.
равны нулю.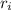 не может содержать больше одного ненулевого элемента, следовательно есть ещё одна строка
не может содержать больше одного ненулевого элемента, следовательно есть ещё одна строка 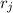 , содержащая второй ненулевой элемент.
, содержащая второй ненулевой элемент.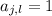 .
.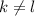 (
(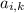 и
и 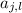 не находятся в одном столбце).
не находятся в одном столбце).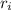 и
и 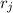 - линейно независимы (докажем это и получим ранг не меньше двух)
- линейно независимы (докажем это и получим ранг не меньше двух)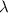 , что
, что 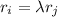 , в частности:
, в частности: 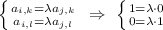
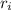 и
и 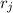 - линейно независимы.
- линейно независимы.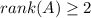
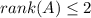 .
.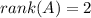 . Других вариантов для матрицы
. Других вариантов для матрицы 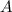 нет.
нет.
Для начала вычислим сколько свеклы:
68*10=680 кг
Далее
780-680=100кг - это сколько лука осталось из общей суммы.
Ящиков-5
Значит
100/5=20 кг
ответ:
В ящике - 20 кг лука