Пошаговое объяснение:
Пусть всего детей было n, и у родителей по одному ребенку.
Событие A="Хотя бы один ребенок получит подарок от своих родителей" противоположно событию B="Ни один ребенок не получит подарок от своих родителей". Значит, искомая вероятность 
.
Найдем количество вариантов раздачи подарков, при которых каждый ребенок получит подарок от чужих родителей.
Рассмотрим таблицу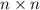 
(см. приложение). Столбец соответствует родителям, строка - детям, выбор ячейки на пересечении i-ой строки и j-ого столбца означает, что i-ый ребенок получил подарок от j-ых родителей [ячейки диагонали не рассматриваются, т.к. получение подарка от своих же родителей - неподходящая ситуация]. Требуется выбрать n ячеек такой таблицы так, чтобы в каждом столбце и строке была выбрана ровно одна ячейка [каждый ребенок получил подарок не от своих родителей, и каждый родитель вручил подарок не своему ребенку].
А это известная задача о расстановке ладей, не бьющих друг друга и не находящихся на одной из диагоналей, для которой было получено явное выражение числа вариантов [подробнее, например, Окунев Л. Я. Комбинаторные задачи на шахматной доске. — 1935 , с .8-14]
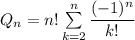
Всего вариантов раздачи подарков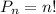 
.
Но тогда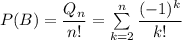 
.
Отсюда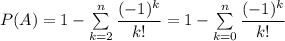 
________________________
Теперь рассмотрим ситуацию при 
Используя разложение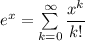 
, получим при 
равенство
.
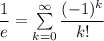Значит,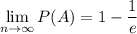 
120А
700Б
540С