Канистра с бензином имеет массу 22 кг. если она заполнена на половину, ее масса 12 кг. какова масса - id306966520210414 от assikissa987614 14.04.2021 01:00

Question

Математика: Канистра с бензином имеет массу 22 кг. если она заполнена на половину, ее масса 12 кг. какова масса пустой канистры?

assikissa987614 · Accepted Answer

Смотри, я думаю базу писать незачем, сам проверишь
1)

$2^{3^{k} } +1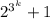$ кратно 3 (предположение )

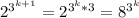$2^{3^{k+1} } = 2^{3^{k}*3 }=8^{3^{k} }$ будем смотреть по модулю три. 8 дает остаток два, значит можем понизить оснавание степени 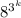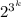$8^{3^{k} }$ ≡ $2^{3^{k} }$ (mod 3) отсюда следует что

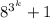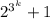$8^{3^{k} }+1$ ≡ $2^{3^{k} } +1$ ≡0(mod 3) по предположению

2)

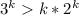$3^{k}k*2^k$ (предположение)

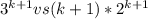$3^{k+1} vs (k+1)*2^{k+1}$ vs это тип мы не знаем какое число больше

поделим каждую часть на два

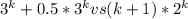
$3^{k}+0.5*3^{k} vs (k+1)*2^{k}$

раскроем скобки

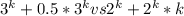
$3^{k}+0.5*3^{k} vs 2^{k}+2^k*k$

скоращаем 3^k и (2^k)*k по предположению

домножим все на 2 и получим

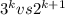
$3^{k} vs 2^{k+1}$
что логично верно при любом к>1 (можно тоже по индукции доказать) ну или просто, что мы увеличивая к на 1 домножаем левую часть на 3 а правую на 2
Ну а случай к=1 можно проверить просто подставив
(решение не самое красивое)

Канистра с бензином имеет массу 22 кг. если она заполнена на половину, ее масса 12 кг. какова масса пустой канистры?

MOGZ ответил