а) на доске выписаны числа 1, 2, 4, 8, 16, 32, 64, 128. разрешается стереть любые два числа и вместо них выписать их разность – неотрицательное число. после семи таких операций на доске будет только одно число. может ли оно равняться 97?
б) на доске выписаны числа 1, 21, 2², 2³, 210. разрешается стереть любые два числа и вместо них выписать их разность – неотрицательное число. после нескольких таких операций на доске будет только одно число. чему оно может быть равно?
решение
a) получить 97 можно, например, так. последовательно вычитая из 16 числа 8, 4, 2, 1, получим 1. на доске остались числа 1, 32, 64, 128. далее: бикю 64 – 32 = 32, 32 – 1 = 31, 128 – 31 = 97.
б) докажем, что если на доске выписаны числа 1, 2, 2n, то после n операций, описанных в условии, может получиться любое нечётное число от 1 до 2n – 1. очевидно, числа, большие 2n, на доске не появляются. легко видеть также, что на доске всегда присутствует ровно одно нечётное число. значит, и последнее оставшееся на доске число нечётно. утверждение о том, что все указанные числа построить можно, докажем индукцией по n.
база. имея числа 1 и 2, можно получить только число 1.
шаг индукции. пусть на доске выписаны числа 1, 2, 2n+1. любое нечётное число, меньшее 2n, можно получить за n + 1 операцию (на первом шаге сотрём 2n+1 и 2n и напишем 2n, далее по предположению индукции). нечётные числа от 2n + 1 до 2n+ 1 – 1 можно записать в виде 2n+1 – a, где число a можно получить из набора 1, 2, 2n. на последнем шаге из 2n+1 вычитаем a.
ответ
а) может; б) любому нечётному числу от 1 до 210 – 1.
замечания
: 2 + 3
Пошаговое объяснение:
1) с первым интегралом все достаточно просто
здесь мы перейдем к повторным интегралам и получим вот что
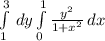
сначала вычисляем внутренний интеграл
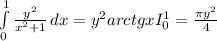
теперь вычисляем внешний интеграл
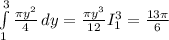
это и есть ответ 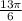
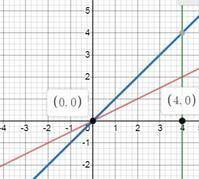
2) со вторым придется построить графики, чтобы определить границы интегрирования по х
тут мы видим, что х изменяется 0≤х≤4
в общем-то нижний предел интегрирования можно было бы найти и путем выяснения, в какой точке пересекаются графики (через уравнение х/2 = х корень данного уравнения х=0), но лучше все же строить график
теперь, собственно приступаем к переходу и интеграции
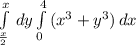
внутренний интеграл
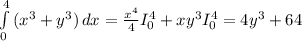
внешний интеграл
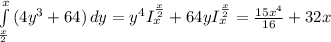
ответ 
Смотри, НАПРИМЕР одна сторона 4см, а вторая 3см, тогда S=4х3=12 см2. При увеличении 4 на 30% =5,2 и уменьшая 3 на 40% = 1,8. Тогда S=5,2х1,8=9,36 см2.
12-22%=9,36 см2