![(1;\sqrt{2}]](/tpl/images/0307/4581/75b91.png)
Пошаговое объяснение:

Здесь  острый угол прямоугольного треугольника, то есть
острый угол прямоугольного треугольника, то есть

Функция  возрастает на
возрастает на ![(\frac{\pi}{4};\frac{\pi}{2}]](/tpl/images/0307/4581/a67df.png) и убывает на
и убывает на  при этом
при этом  поэтому множеством значений этой функции на указанном промежутке является множество
поэтому множеством значений этой функции на указанном промежутке является множество ![(\frac{\sqrt{2}}{2};1],](/tpl/images/0307/4581/c9598.png) откуда множеством значений функции
откуда множеством значений функции  на указанном промежутке является множество
на указанном промежутке является множество ![(1;\sqrt{2}].](/tpl/images/0307/4581/af522.png)
Разбиваем промежуток на 10 частей (шаг = 2/10 = 0,2).
Находим значение функциив каждой точке.
Определяется площадь элементарного участка как произведение полусуммы крайних значений функции на данном участке на шаг.
В итоге суммируются все 10 участков.
При данном ошибка составила 1,2%.
Метод трапеций
x = 0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2
y = (4-x^2)^(1/2) 2 1,989974874 1,959591794 1,907878403 1,833030278 1,732050808 1,6 1,428285686 1,2 0,871779789 0 3,141592654
Площадь 0,398997487 0,394956667 0,38674702 0,374090868 0,356508109 0,333205081 0,302828569 0,262828569 0,207177979 0,087177979 3,104518326 0,037074327 0,011801125
Лучше изображение смотреть в фото.

(см. объяснение)
Пошаговое объяснение:
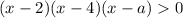
Решим параметр в координатах (x; a). Для этого строим прямые x=2, x=4 и a=x. Далее просчитаем знаки в образовавшихся областях (можно применить правило, что через точку знаки сохраняются). Получим то, что показано в прикрепленном файле. Теперь будем двигать горизонтальную прямую до тех пор, пока не добьемся интересующего нас случая (красная линия). Этот случай достигается, когда горизонтальная прямая проходит через точку пересечения прямых x=2 и a=x, то есть искомая координата (2; 2). Получили, что при a=2 множество решений исходного неравенства является одним промежутком.
Задание выполнено!
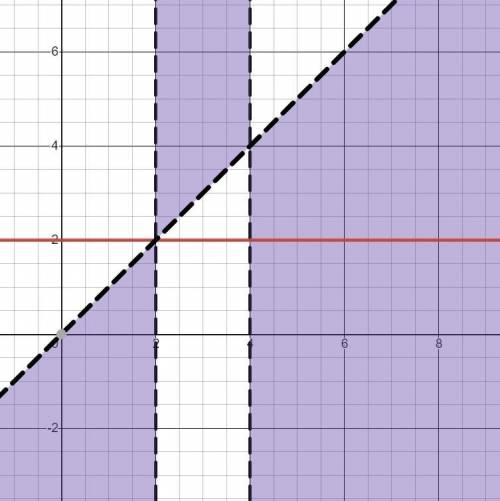
(1; √2]
Пошаговое объяснение:
Пусть a, b - катеты прямоугольного треугольника, а с - его гипотенуза.
Отношение суммы катетов к гипотенузе имеет вид:
(a + b)/c = a/c + b/c = sinα + cosα, где α - угол в исходном треугольнике (всегда острый, I четверть).
Функция у = sinα + cosα на отрезке [0; π/2] имеет максимум в точке π/4 со значением √2. Это верхний предел искомого отношения.
Нижний предел равен 1 (в точках 0 и π/2).
Таким образом, искомое соотношение лежит в пределах от 1 до √2, не достигая нижней границы интервала.