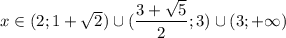1. 10 м
2. 5 м
3. 60 м
Пошаговое объяснение:
S = 4S(полукруга)+S(квадрата)
Пусть 2a - длина стороны квадрата, тогда радиус полукруга в 2 раза меньше и равен а.
S(полукруга) = 
*r^2/2, где r - радиус полукруга.
4S(полукруга) = 4*а^2/2 = 2*а^2
S(квадрата) = (2a)^2 = 4a^2
Общая площадь S = 4S(полукруга)+S(квадрата) = 2*а^2 + 4a^2 =
= 6a^2 + 4a^2 = 10a^2 = 250 м²
Тогда а = 5 м - длина радиуса полукруга
2а = 10 м - длина стороны квадрата
Забор состоит из 4 полукругов, значит, его длина
4*2r/2 = 4r = 4a = 4*3*5 = 60 м
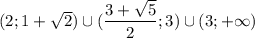
Пошаговое объяснение:
ОДЗ логарифмов: x > 0, x ≠ 1, x > 2, x ≠ 3 ⇒ x > 2, x ≠ 3
Пусть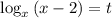 
. Тогда 
:
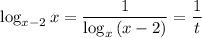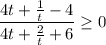. Заметим, что t ≠ 0, так как это значение достигается только при x = 3 (x - 2 = x⁰ = 1 ⇔ x = 3). Но при x = 3 основание логарифма 
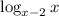равно 1, что не удовлетворяет ОДЗ. Значит, домножим обе части дроби на t:
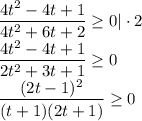
Решим методом интервалов:
+ - + +
----o----o----*---->
-1 -¹/₂ ¹/₂
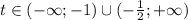
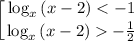
Заметим, что по ОДЗ x > 2, то есть основание логарифма всегда больше 1. Значит, на ОДЗ неравенства равносильны:
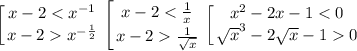
Первое неравенство имеет решение (с учётом ОДЗ)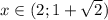 
Второе неравенство раскладывается на множители:
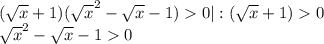
Нули получившегося неравенства: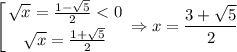 
C учётом ОДЗ получаем, что в данном случае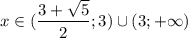 
(левая граница меньше правой, так как √5 < 3).
Объединим промежутки. Сравним правую границу первого неравенства и левую границу второго. Сравним эти числа относительно 2,5:
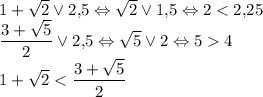
Тогда промежутки не пересекаются, итоговый ответ: 
