ответ:Чтобы решить это уравнение, разделите знаменатели на множители и с квадратичной формулы найдите два действительных корня, которые дадут значение x.
Пошаговое объяснение:
Чтобы решить это уравнение, нужно разложить знаменатели дробей. Уравнение имеет вид 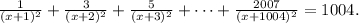 Затем мы можем умножить обе стороны уравнения на
Затем мы можем умножить обе стороны уравнения на  и разложить левую часть, в результате чего получим полиномиальное уравнение степени 1004. Чтобы решить это уравнение, нам нужно воспользоваться квадратичной формулой для нахождения корней многочлена. В результате мы получим два вещественных корня, которые и дадут значение x.
и разложить левую часть, в результате чего получим полиномиальное уравнение степени 1004. Чтобы решить это уравнение, нам нужно воспользоваться квадратичной формулой для нахождения корней многочлена. В результате мы получим два вещественных корня, которые и дадут значение x.
Квадратичная формула - это математическое уравнение, используемое для решения корней полиномиального уравнения степени два. Она гласит, что для любого квадратного уравнения. 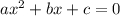 два корня можно найти по следующей формуле: x = (-b ± √(b^2 - 4ac)) / 2a, где a, b и c - коэффициенты полиномиального уравнения. Знак ± указывает на то, что уравнение может иметь два различных решения в зависимости от выбранного знака.
два корня можно найти по следующей формуле: x = (-b ± √(b^2 - 4ac)) / 2a, где a, b и c - коэффициенты полиномиального уравнения. Знак ± указывает на то, что уравнение может иметь два различных решения в зависимости от выбранного знака.
х max = -1/3; x min = 0
Пошаговое объяснение:
Исследовать функцию на экстремумы и нарисовать её график.

Найдем производную, приравняем к нулю и найдем корни. Отметим их на числовой оси и определим знаки производной на промежутках.
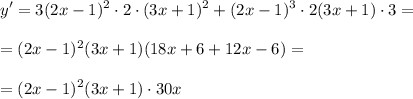
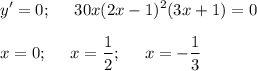
См. вложение.
Если "+" - функция возрастает, если "-" - функция убывает.Функция возрастает на промежутках: (-∞; -1/3]; [0; +∞).
Убывает на промежутках: [-1/3; 0]
Если производная меняет знак с плюса на минус, то в данной точке наблюдается максимум, если с минуса на плюс, то в данной точке - минимум.х max = -1/3; x min = 0
y(-1/3) = 0; y(0) = -1
Обозначим эти точки на координатной плоскости и нарисуем график.
