решение на фотографиях
Пошаговое объяснение:
1) Линейное ДУ. Используем замену.
2) Однородное ДУ. Используем замену.
3) ДУ 2 порядка, допускающее понижение порядка. Используем замену.
4) Неоднородное линейное ДУ. Решено с метода неопределенных коэффициентов. Первым действием решаем ОЛДУ (однородное линейное ДУ). Вторым подбираем y~, дифференцируем, подставляем все это в НЛДУ, находим. В ответе к у из 1) прибавляем у~ из 2).
5) Все то же НЛДУ, но уже решаем методом вариации произвольных постоянных. Постаралась вкратце формулами расписать, надеюсь, понятно. Находим главный определитель (W), а в W1 и W2 на месте 1 и 2 столбцов подставляем значения независимых членов, без переменных (Z'1(x) и Z'2(x)), я их выделила черным цветом. И еще сначала искала Z2(x), так как ошиблась со столбцом. Нашли определитель - его значение и будет являться Z'(1 или 2)(х). Осталась интегрировать, чтобы найти функцию без '. Готово. Не забываем прибавить ту часть функции, которую нашли в 1), и записываем ответ.
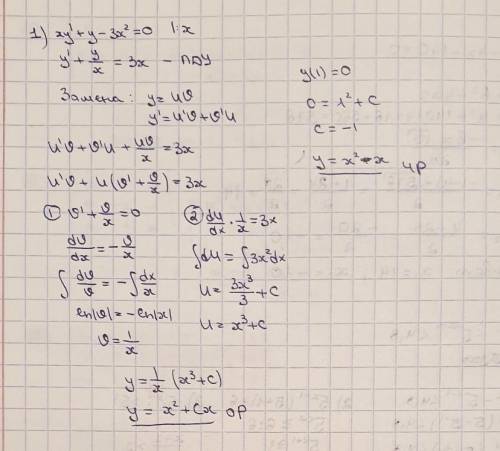



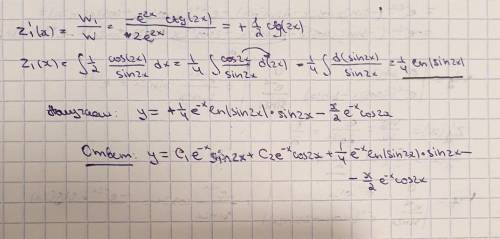
"5"-1/7
"4"-1/3
"3"-1/2
"2"-?
Количество учащихся должно делится на 7,на 3 и на 2.
7*3*2=42(уч)-количество учащихся
"5"-42:7=6(ч.)
"4"-42:3=14(ч.)
"3"-42:2=21(ч.)
6+14+21=41(ч.)-получили "5","4" и "3"
42-41=1(уч)-получил "2".
1/7+1/3+1/2=6/42+14/42+21/42=41/42-получили "5","4", и "3".
1-41/42=1/42-получили "2"
42:42=1(уч.)-получил "2".
ответ:1 ученик.