в первой - 34 карандаша, во второй 17 карандашей, в третьей 85 карандашей.
Пошаговое объяснение:
всего 136 карандашей.
во второй коробке - х карандашей.
в первой коробке в 2 раза больше, значит - 2х карандашей.
в третьей коробке в 5 раз больше, чем во второй, значит - 5х карандашей.
получается, что в трёх коробках х + 2х + 5х = 136 карандашей.
решим уравнение:
х + 2х + 5х = 136
8х = 136
х = 17
Х карандашей было во второй, значит во второй 17.
в первой в два раза больше, чем во второй, значит 17*2=34 карандаша.
в третьей в 5 раз больше, чем во второй, значит 17*5=85 карандашей.
Пошаговое объяснение:
1) с первым интегралом все достаточно просто
здесь мы перейдем к повторным интегралам и получим вот что
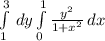
сначала вычисляем внутренний интеграл
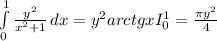
теперь вычисляем внешний интеграл
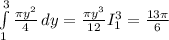
это и есть ответ 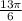
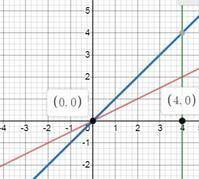
2) со вторым придется построить графики, чтобы определить границы интегрирования по х
тут мы видим, что х изменяется 0≤х≤4
в общем-то нижний предел интегрирования можно было бы найти и путем выяснения, в какой точке пересекаются графики (через уравнение х/2 = х корень данного уравнения х=0), но лучше все же строить график
теперь, собственно приступаем к переходу и интеграции
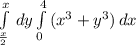
внутренний интеграл
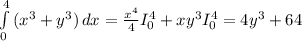
внешний интеграл
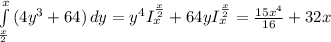
ответ 
a, b, c - коэффициенты.
Вершина параболы находится по ф-ле:
х = - в / 2а, тогда х, что получится. , подставляем в
уравнение и получаем у. Эта точка с координатами х и у
и будет вершиной параболы.
Во всех примерах b нет, значит b=0 и х=0
а) х=0 у=0+4=4
б) х=0 у=0+4=4
в)х=0 у=0-2=-2
г)х=0 у=0+0,5=0,5