Пошаговое объяснение для 1 задачи:
Периметр прямоугольника = 2*(a+b)
Одну сторону возьмём за x, вторая сторона на 3,8 больше x:
12.4 = 2(x+(x+3.8) (обе стороны поделим на 2)
6,2 = x+x+3.8
6.2 = 2x+3.8 (перенесём известное влево)
2,4 = 2x
x = 1.2 (одна сторона)
x+3.8 = 5 (вторая сторона)
Площадь прямоугольника = a*b = 1.2 * 5 = 6 см²
Пошаговое объяснение для 2 задачи:
Переведём всё в копейки:
15грн 60 к = 1560 к
1 грн 20 к = 120 к
3 ручки + 5 карандашей = 1560 к
Возьмём цену ручки за x. Стоимость карандаша x-120. Составим уравнение:
(3*x) + (5(x-120)) = 1560
Раскрываем скобки:
3x+5x-720=1560
8x=2280
x=285 к = 2грн 85 к (стоимость ручки)
x-120 = 165 к = 1 грн 65 к (стоимость карандаша)
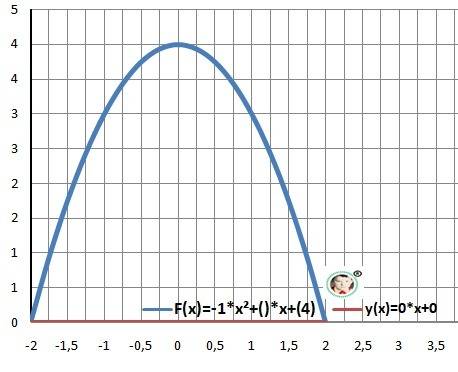
Дано: F(x)=- x²+4, y(x)=0
Найти: S=? - площадь фигуры
Пошаговое объяснение:
1) Находим точки пересечения графиков.
x²-4 = 0 - квадратное уравнение
a = -2- верхний предел, b = 2- нижний предел.
2) Площадь - интеграл разности функций.
f(x) = -4 + x² - подинтегральная функция
3) Интегрируем функцию и получаем:
F(x) = -4*x + 1/3*x³
4) Вычисляем на границах интегрирования.
S(а) = S(-2) = 8 -2,67 = 5,33
S(b) = S(2) = -8 +2,67 = -5,33
S = S(2)- S(-2) = 10,66 - площадь
Рисунок к задаче в приложении.
б)
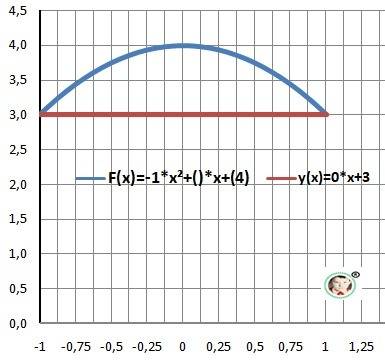
Дано: F(x)= - x² +4, y(x)= 3
Найти: S=? - площадь фигуры
Пошаговое объяснение:
1) Находим точки пересечения графиков.
x² - 1=0 - квадратное уравнение
a = -1- верхний предел, b = 1- нижний предел.
2) Площадь - интеграл разности функций.
f(x) = -1 + x² - подинтегральная функция
3) Интегрируем функцию и получаем:
F(x) = -x+ 1/3*x³
4) Вычисляем на границах интегрирования.
S(а) = S(-1) = 1 - 0,33 = 0,67
S(b) = S(1) =-1 +0,33 = -0,67
S = S(1)- S(-1) = 1,34 - площадь
Рисунок к задаче в приложении.