ответ:1. Две прямые на плоскости могут располагаться либо паралельно друг другу, либо пересекаться, ну или - совпадать.
2. При пересечении двух прямых образуется четыре неразвернутых угла: ∠1, ∠2, ∠3, ∠4.
3. Вертикальные углы — пара углов, у которых вершина общая, а стороны одного угла составляют продолжение сторон другого угла.
4. Свойство вертикальных углов: Вертикальные углы равны.
5. Если они образуют четыре прямых угла.
6. Перпендикулярность прямых (или их отрезков) обозначают знаком перпендикулярности «⊥».
7. Построение перпендикулярной прямой.
Через точку O провести прямую, перпендикулярную данной прямой a.
Возможно два варианта:
точка O лежит на прямой a;
точка О не лежит на прямой a.
1) 3 1/16 - 1/8 = 49/16-2/16 = 47/16 = 2 15/16 (привели дроби к общему знаменателю 16)
2) 7 9/20 - 5 17/30 = 149/20 - 167/30 = 447/60-334/60 = 113/60=1 53/60
(привели дробь к общему знаменателю 60)
3) 4 2/7 - 1 4/9 = 30/7 - 13/9 = 270/63 - 91/63 = 179/63 = 2 53/63 (привели дробь к общему знаменателю 63)
4) 8 5/36 - 1 43/108 = 293/36 - 151/108 = 879/108-151/108 = 728/108 = 6 80/108 = 6 20/27 (привели дробь у общему знаменателю 108. в конце сократили 80/108 на 4 и получили 20/27)
5) 9 7/9 - 4 5/6 = 88/9 - 29/6 = 176/18 - 87/18 = 89/18 = 4 17/18 (привели дробь к общему знаменателю 18)
6) 6 7/32 - 2 11/48 = 199/32 - 107/48 = 597/96 - 214/96 = 383/96 = 3 95/96
Пошаговое объяснение:
Найдем сначала общее решение соответствующего однородного дифференциального уравнения:
Используя замену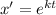 , получим характеристическое уравнение
, получим характеристическое уравнение
Общее решение однородного дифференциального уравнения:
Рассмотрим функцию: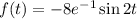 . Здесь
. Здесь 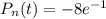 откуда
откуда 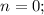 и
и 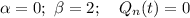 . Сравнивая α, β с корнями характеристического уравнения, частное решение будем искать в виде:
. Сравнивая α, β с корнями характеристического уравнения, частное решение будем искать в виде:
Подставляем в исходное дифференциальное уравнение:
Приравниваем коэффициенты при cos2x и sin2x, получаем систему:
Общее решение линейного неоднородного дифференциального уравнения:
Осталось решить задачу Коши, подставляя начальные условия
Частное решение задачки Коши: