Пошаговое объяснение:
( 400 :X + 5 ) - 5 = 200
400 : x + 5 = 200+5
400:x + 5 = 205
400 : x = 205 - 5
400 : x = 200
x = 400 : 200
x = 2
1000 - ( 4500 :X + 80 ) = 420
4500:x + 80 = 1000-420
4500:x + 80 = 580
4500:x = 580 - 80
4500:x = 500
x = 4500:500
x = 9
(54 :X + 30 ) x 2 = 72
54:x + 30 = 72:2
54:x + 30 = 36
54:x = 36 - 30
54:x = 6
x = 54 : 6
x = 9
8 * ( 36 + 4*X) = 480
36 + 4x = 480:8
36 + 4x = 60
4x = 60 - 36
4x = 24
x = 24 : 4
x = 6
(6*X + 12 ) : 6 = 50
6x + 12 = 50 * 6
6x + 12 = 300
6x = 300 - 12
6x = 288
x = 288 : 6
x = 48
Объясняю, как я это получил:
Выразим y из обоих уравнений.Выполним необходимые расчеты.Запись на языке математики:
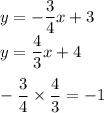
Это упростит нам задачу и даст возможность пользоваться формулой:
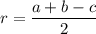
Это удобнее, чем считать по, например, этой формуле:
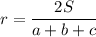
Введем систему координат, как показано на рисунке (см. прикрепленный файл)
Определим координаты вершины треугольника. Замечу, что в случаях, где важна точность НЕ ДОПУСТИМ графический метод! Поэтому будем поочередно брать 2 уравнения и записывать систему.
Пример для первой вершины:
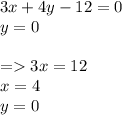
Координата первой вершины - (4; 0).
Аналогично находим координаты двух других вершин:
(-3; 0) и (-0.48; 3.36)
Теперь найдем стороны треугольника:
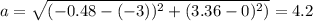
Аналогично:
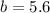
Последняя сторона находится проще:
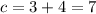
Применим формулу, о которой я упоминал выше и найдем радиус вписанной в треугольник окружности:
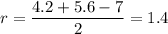
Радиус вписанной в треугольник окружности равен 1.4;
Второй этап решения:
Найдем центр вписанной окружности в треугольник. Найдем длину отрезка, соединяющего вершину треугольника (не при прямом угле) с центром вписанной в него окружности. Проведем радиус к касательной. Он ей перпендикулярен. Вычислим длину катета получившегося прямоугольного треугольника:
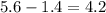
По теореме Пифагора:
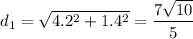
Эту же длину можно получит следующим образом:
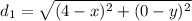
Получили уравнение с 2-мя неизвестными:
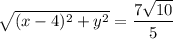
Если мы получим второе уравнение с такими же неизвестными, то сможем решить систему и получить ответ.
Найдем длину отрезка, соединяющего другую вершину треугольника с центром окружности. Проведем радиус к касательной. Он ей перпендикулярен. Вычислим длину катета получившегося прямоугольного треугольника:
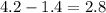
По теореме Пифагора:
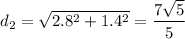
Эту же длину можно получит следующим образом:
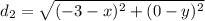
Получили новое уравнение с 2-мя неизвестными:
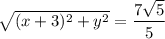
Получили систему уравнений:
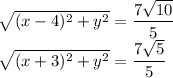
Система легко решается возведением в квадрат обоих частей обоих уравнений.
В результате получили две пары точек:
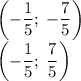
Очевидно, что центр вписанной в треугольник окружности лежит внутри этого треугольника.
Поэтому центр вписанной в треугольник окружности имеет координаты:
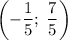
b - 2 chislo
c - 3 chislo
abc=240
ab=60
bc=80
a=60/b
c=80/b
(60/b)*b*(80/b)=240
4800/b=240
b=4800/240=20
c=80/20=4
a=60/20=3