Часто процесс решения неравенств представляет собой переход от исходного неравенства к неравенствам, имеющим те же решения, но которые проще найти. Другими словами, исходное неравенство с определенных преобразований заменяется так называемым равносильным неравенством, решение которого совпадает с решением исходного, и которое мы можем отыскать. В этой статье мы как раз поговорим о равносильных неравенствах и о равносильных преобразованиях, позволяющих получать равносильные неравенства.
Пошаговое объяснение:
надеюсь правельно
1) Точка А =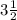 
, а точка В = 
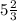⇒ расстояние между ними равно В - А
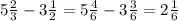
2) Натуральными числами называют целые числа, использующиеся при счёте
Нужно чтобы числа соответствовали неравенству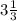 
< x < 7
Т.к. 3<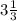 ⇒ нам нужна сумма чисел от 4 до 7, то есть 4 ≤ x < 7
4+5+6 = 15
3) Среднее арифметическое находится сложением данных чисел и делением их на их количество
а)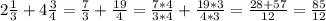 
б)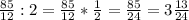 
4) Действуем аналогично как в 3 задании
а)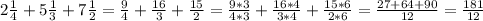 
б)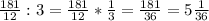 
5) Действуем аналогично как в 2 задании
Нужно чтобы числа соответствовали неравенству 1 < x < 47,5
Т.к. 47,5 < 48 ⇒ нам нужно посчитать количество целых чисел от 1 до 47, то есть 1 < x ≤ 47
Их 46
