Мотоциклист 90 км и велосипедист 30 км
Пошаговое объяснение:
Условие задачи:
Из двух пунктов, расположенных на расстоянии 120 км, одновременно на встречу друг-другу начали двигаться мотоциклист и велосипедист. Скорость мотоцикла на 20 км/час больше чем скорость велосипедиста. Если они встретились через 3 часа, то какое расстояние преодолел каждый из них?
Решение.
Пусть скорость велосипедиста x км/час, то, по условию скорость мотоцикла на 20 км/час больше, то есть (x+20) км/час.
Расстояние S, которое преодолеет объект со скоростью v за время t связаны формулой:
S = v · t .
Через t = 3 часа мотоциклист и велосипедист преодолеют расстояние, соответственно S1 и S2. Тогда:
S1 = (x+20) км/час · 3 часа = 3 · (x+20) км
S2 = x км/час · 3 часа = 3 · x км.
Так как они встретились, то в сумме преодолели расстояние 120 км:
3 · (x+20) + 3 · x = 120
3 · x + 60 + 3 · x = 120
6 · x = 120 - 60
6 · x = 60
x = 60:6 = 10
Значит, скорость велосипедиста 10 км/час, а скорость мотоциклиста 10+20 км/час = 30 км/час.
Тогда каждый из них преодолел расстояние
S1 = 30 км/час · 3 часа = 90 км
S2 = 10 км/час · 3 часа = 30 км.
а) пропорция будет следующая:
100 % - 7
x % - 5
Отсюда х=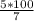 
х=500\7=71
процентов
б) 100 % - 5
х % - 7
Отсюда х = 7 * 100 \ 5 = 700\5 = 140 процентов
в) из пункта б мы видим, что число 7 составляет 140 процентов, а 5 - 100 процентов,соответсвенно,то есть на 40 процентов число 7 больше числа 5
г) из пункта а) мы видим,что число 5 составляет 71 процента от числа 7,то есть 100 - 71 процентов = 100 -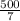 
= 700-500\7=200\7 (выражаем целую часть - получаем:
28 
Считал без калькулятора,методом деления уголком)
