Путешественник ехал на автомобиле 480/х часов, где х - скорость езды на автомобиле
Путешественник ехал на велосипеде 30/y часов, где y - скорость езды на велосипеде
Путешественник ехал на велосипеде на 6 часов меньше. чем на автомобиле:
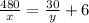
Расстояние, пройденное за время езды на автомобиле со скоростью велосипеда:
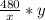
расстояние, пройденное за время езды на велосипеде со скоростью автомобиля:
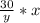
Последние два выражения равны:
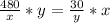
Пусть а=y/x, тогда:
480а=30/а
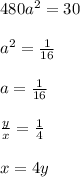
Подставляем в первое уравнение:
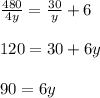
y=15 км/ч - скорость перемещения на велосипеде.
Значит, путешественник ехал на велосипеде 30/15=2 часа
умножим второе на (-5) и сложим с первым
17у+34=0 ⇒ у=-2 тогда х=4у+4=4·(-2)+4=-4
Назовем точку
А(-4;-2)
умножим второе на (-5) и сложим с первым
17у=0 ⇒ у=0 тогда х=4у+4=4·0+4=4
Эта точка С(4;0)- она противоположна точке А
Найдем координаты середины отрезка АС
О(0;-1)
Диагонали ромба взаимно перпендикулярны и делятся в точке пересечения пополам.
Уравнение второй диагонали запишем как уравнение прямой, перпендикулярной х-4у-4=0
или у=(1/4)х-1.
Известно, что угловые коэффициенты взаимно перпендикулярных прямых при умножении дают -1:
у=-4х+b - общий вид прямых, перпендикулярных х-4у-4=0
Для нахождения b подставим координаты точки О:
-1=-4·0+b ⇒ b=-1
y=-4x-1 или 4х+у+1=0 - уравнение второй диагонали
Найдем точки пересечения данных прямых с этой диагональю
умножим второе на (3) и сложим с первым
17х+17=0 ⇒ x=-1 тогда y=-4x-1=-4·(-1)-1=-1=3
Назовем точку
B(-1;3)
умножим второе на (3) и сложим с первым
17x-17=0 ⇒ x=1 тогда y=-4x-1=-4·1-1=-5
Эта точка D(1;-5)- она противоположна точке B
Уравнение стороны ВС находим по формуле для составления уравнения прямой, проходящей через две точки:
3(x-4)=-5y ⇒3x+5y-12=0
Уравнение стороны AD находим по формуле для составления уравнения прямой, проходящей через две точки:
3(x-1)=-5(y+5) ⇒3x+5y+22=0