1) Дать определение: число a больше числа b
a > b, ели a − b > 0
Число a больше числа b, если разность этих чисел положительна.
2) Сравнить:
а)
8/11 и 9/13
Вычтем из первого числа второе:
 и 0
и 0
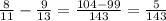
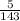 и 0
и 0
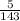 > 0
> 0
Значит, 
б)
a²+16 и 8a
Вычтем из первого выражения второе:
a²−8a+16 и 0
(a−4)² и 0
по определению, вырежение в квадрате всегда дает число неотрицательное, то есть (a−4)²≥0
(a−4)² = 0, если a = 4
(a−4)² > 0, если a ≠ 4
Значит, a² + 16 > 8a, если a ≠ 4; и a²+16 = 8a, если a = 4.
3) Доказать неравенство:
(a−3)(a+11) < (a+3)(a+5)
a²+11a−3a−33 < a²+5a+3a+15
Вычтем из первого выражения второе:
a²+11a−3a−33−a²−5a−3a−15 и 0
−48 и 0
Значит, (a−3)(a+11) < (a+3)(a+5), что и требовалось доказать.
4) Сравнить числа а и b, если верно неравенство: 3a−3b ≥ 1
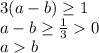
5) Оценить величину: 5а−2, если 1,1 < а ≤ 1,2
Умножим все части неравенства на 5:
5·1,1 < 5a ≤ 5·1,2
5,5 < 5а ≤ 6
Вычтем из всех частей неравенства 2:
5,5−2 < 5а−2 ≤ 6−2
Получаем:
3,5 < 5а−2 ≤ 4
Каждую из этих фраз он мог сказать про мальчика или про девочку.
1. Если первую фразу он сказал применительно к мальчику, то у него было 7 сыновей: этот самый мальчик и его шесть братьев.
1.1. Если вторую фразу он сказал тоже про мальчика, то у этого мальчика сестер, как и братьев по 6. Итого: 6+6+1=13 детей
1.2. Если вторую фразу он сказал про девочку, то у нее братьев будет 7, а значит и сестер тоже 7. Итого: 7+7+1=15 детей
2. Если первую фразу он сказал применительно к девочке, то у него было только 6 сыновей.
2.1. Если вторую фразу он сказал про мальчика, то у этого мальчика будет только 5 братьев, соответственно сестер столько же. Итого: 5+5+1=11 детей
2.2. Если вторую фразу он сказал про девочку, то у нее 6 братьев и соответственно 6 сестер. Итого: 6+6+1=13 детей
Максимальное количество детей - 15
ответ: 15
Итак, в правом кармане было 7 орехов, тогда в левом кармане был 7*3=21 орех.
ответ: в правом кармане -- 7 орехов; в левом кармане -- 21 орех.