Пошаговое объяснение:
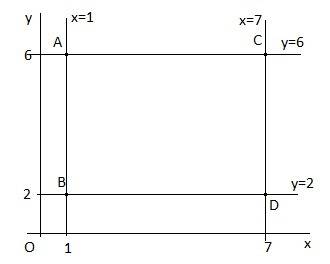
Отметим точки A, B и C на координатной плоскости. У точек A и B совпадают абсциссы точек, соединяем их прямой x = 1.
У точек A и C совпадают ординаты точек, соединяем их прямой y = 6.
Через точку B с ординатой 2 проводим прямую y = 2 параллельную прямой y = 6 (противоположной стороне прямоугольника).
Через точку C с абсциссой 7 проводим прямую x = 7 параллельную прямой x = 1 (противоположной стороне прямоугольника).
Проведенные через точки B и C прямые пересекутся в точке D(7; 2), которая и будет 4 вершиной прямоугольника ABCD.
Применяем группировки:
a²+2ab+b²-c²+4cd-4d²=(a²+2ab+b²)-(c²-4cd+4d²)=
применяем формулы сокращенного умножения m²±2mn+n²=(m±n)²
=(a+b)²-(c-2d)²=
применяем формулу разности квадратов m²-n²=(m-n)(m+n)
m=a+b
n=c-2d
=(a+b-c+2d)(a+b+c-2d) - о т в е т.