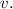Тогда скорость Феди равна 
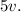Когда Федя догоняет Соню, их скорость сближения равна 
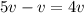(вычитаем, поскольку Соня уходит от догоняющего её Феди, тем самым, как бы мешая ему себя догонять). Когда Федя в очередной раз обгоняет Соню, его удалённость от Сони, которую он встретит в будущем, в следующем месте обгона, составляет как раз один круг. За время, пока Федя доедет до нового обгона Сони, Соня пройдет по круговой дорожке в 4 раза меньшее расстояние, поскольку её скорость в 4 раза меньше скорости сближения. Из этого и следует, что за время между двумя очередными последовательными встречами, которые разделяют участников движения расстоянием в один круг, Соня проходит только четверть круговой дорожки. Значит за 4 дополнительные встречи (после первой начальной) она и пройдёт полный круг. Т.е. всего существует 4 места, в которых малыш Федя обгоняет Соню на ходулях.
Пошаговое объяснение:
Задача №1
Пусть искомые дроби будут 1/х и 1/у, тогда
2/7=1/х+1/у
2/7=(у+х)/ху
Получаем систему
х+у=2
ху=7
х=2-у, тогда
(2-у)у=7
2у-у²-7=0
y²-2y+7=0
D=-2²-4*7=4-28=-24
Поскольку дискриминант отрицательный, значит уравнение решений не имеет.
ответ: нельзя представить.
Задача №2
Пусть производительность ученика х, тогда производительность токаря 2х. Общая производительность будет (х+2х) Время на выполнение задания 9 часов. Время работы ученика будет t, а время работы токаря (9-t) . При одновременной работе задание выполняется за 4 часа , можем составить уравнение
n/(x+2x)=4,
где n- задание, которое надо выполнить.
n/(x+2x)=4
n/3x=4
n=12x
При работе по очереди получим
xt+2x(9-t)=12x
xt+18x-2xt-12x=0
6x- xt=0
x(6-t)=0
x=0
6-t=0
t=6 часов время работы ученика
9-6=3 часа время работы токаря.
Учитывая , что производительность труда токаря в 2 раза больше, значит ученик выполнил половину работы.
ответ:1/2 часть работы выполнил ученик
Задача №3
попаданий в 10 было четыре , значит 4*10=40 очков
90-40=50 очков набрал при попадании в 7,8 и 9
За остальные шесть выстрелов он мог попасть в семерку, восьмерку и девятку 7+8+9=24 очка, остается 50-24=26 очков и три выстрела. Значит он мог попасть 8+9+9=26 очков.
ответ: 1 раз в семерку, два раза в восьмерку и три раза в девятку
Задача №4
При правильной игре выиграет первый игрок. Пусть первый игрок берет по 99 монет , а второй по 100 монет, тогда через 20 ходов, на столе останется
2005-(10*99+10*100)=15 монет. В любом случае в конце на столе будет оставаться нечетное количество монет. Последний ход будет первого игрока , а он может брать нечетное число монет. Значит он выиграет.
Задача №5
Попробуем вычислить сколько воды будет после нескольких переливаний
1).1-1/2=1/2
2)1/2+1/3=5/6
3)5/6-1/3=3/6=1/2
4)1/2+1/4=3/4
5)3/4-1/4=1/2
6)1/2+1/6=4/6=2/3
7)2/3-1/6=3/6=1/2
8)1/2+1/8=5/8
9)5/8-1/8=4/8=1/2
Как видим сколько забираем из сосуда , столько же и возвращаем в него на нечетном шаге. У нас всего 2007 переливаний, цифра 2007 нечетная, следовательно на 2007 шаге в сосудах будет по ½ л воды
четвёртом