а) 49+(-23) 49-23=26
б) 56+(-63)=56-63=-7
Пошаговое объяснение:
Начальная температура: t₁ = -6°C
Через 1 минуту: t₂ = - 6°C - 9°C = - 15°С
Через 2 минуты: t₃ = - 15°С - 9°С = -24°С
Через 3 минуты: t₄ = - 24°С - 9°С = -33°С
Через 4 минуты: t₅ = - 33°С - 9°С = -42°С
Через 5 минут: t₆ = - 42°С - 9°С = -51°С
Через 6 минут: t₇ = - 51°С - 9°С = -60°С
Плохое решение.
Заметим, что мы имеем дело с арифметической прогрессией, в которой:
a₁ = - 6°C
d = - 9°C
n = 7
Тогда:
a₇ = a₁ + (n - 1)·d = -6°C + (7 - 1)·(-9°C) = - 60°C
Получены следующие значения случайной величины :
11 7 13 15 11 9 13 1 13 11 7 13 15 1 13 11 7 13 11 15 11 13 7 9 11 13 9 17 13 15 7 11 9 15 13 9 17 11 9 15 17 9 15 13 13 15 17 9 1 13.
Элементы статистики:
16 размах
11,32 среднее
13 мода
12 медиана
Найдены повторяющиеся элементы и их частота:
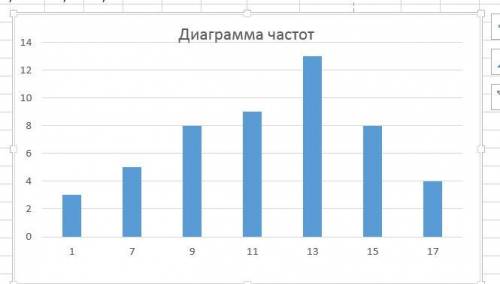
Значения 1 7 9 11 13 15 17
Частота 3 5 8 9 13 8 4
Вычислим среднее значение: 1*3+7*5+9*8+11*9+13*13+15*8+17*4 = 566
Среднее значение равно 566/50 = 11,32.
Вычисляем квадраты отклонений от среднего значения:
(1-11,32)2 = 106,50
(7-11,32)2 = 18,662
(9-11,32)2 = 5,382
(11-11,32)2 = 0,102
(13-11,32)2 = 2,822
(15-11,32)2 = 13,54
(17-11,32)2 = 32,26
Вычислим среднее арифметическое (дисперсию) этих значений:
σ^2=(106.50+18.662+5.382+0.102+2.822+13.54+32.26)/7=25,6097. Стандартное отклонение равно квадратному корню дисперсии:
σ=√25,6097=5,0606.
а)49+(-23)=49-23=26
б)56+(-63)=56-63=-7