Пусть из А выезжает велосипедист со скоростью х км в час.
Из B выезжает мотоциклист со скоростью y км в час.
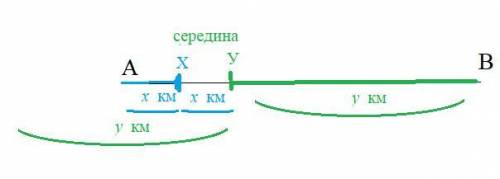
За первый час велосипедист проехал х км в сторону В и оказался на расстоянии х км от мотоциклиста в точке Х, который проехал у км и оказался в точке Y
За второй час велосипедист проедет еще х км и окажется в точке Y,
которая расположена на расстоянии 2х км от А.
За второй час мотоциклист проедет еще у км и окажется в точке Z, расположенной от точки А на таком же расстоянии 2х км
Таким образом мотоциклист за час проезжает путь YA, равный 2х км и АZ, равный 2х км
т.е мотоциклист проезжает путь 4х за час, значит его скорость в четыре раза больше скорости велосипедиста.
Пошаговое объяснение:
Введем величину "скорость сближения машин" V_сбл, км/час.
Машины встретились через 9 часов, т.е. скорость сближения машин V_сбл. равна:
V_сбл=720 [км]/9 [час] = 80 [км/час].
Чтобы встретиться через 6 часов машины должны увеличить V_сбл. На сколько?
V'_сбл = 720 [км]/6 [час]=120 [км/час].
Т.е. скорость сближения должна увеличиться на 120-80= 40 км/час
Какие скорости были у каждой машины, в задаче ничего не сказано.
Например, если V₁=30 км/час, то V₂=(80-30)=50 км/час. Как скорости изменились? Например стали:
V'₁=50 км/час, V'₂=(120-50)=70 км/час.
Или:
V'₁=10 км/час, V'₂=(120-10)=110 км/час.
1,3м=13 дм
13:5