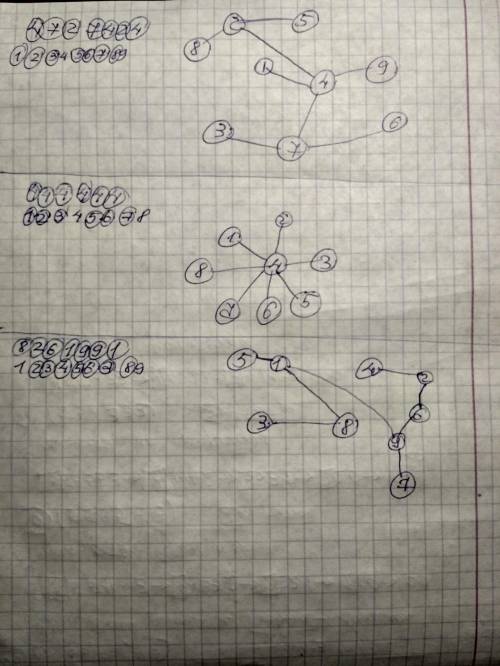
Задание 1
ответ в приложении
Задание 2
Тут, очевидно, опечатка, k<n. В дереве на n вершинах не может быть вершины степени n.
n=1:
k=0 - одно дерево, состоящее из одной вершины.n=2:
k=0 => граф не связный => не деревоk=1 => одно дерево, состоящее из одного ребраn>2:
k=0 => граф не связный => не деревоk>0 => Тогда каждому дереву поставим в соответствие код Прюфера. Его длина - n-2. Т.к. вершина 1 имеет степень k, то встречается в нем k-1 раз. Тогда для остальных n-1 вершин остается n-2-(k-1)=n-k-1 мест. Тогда всего таких кодов Прюфера, и, следовательно, деревьев,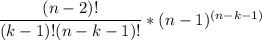
Задание 3
Найти количество деревьев с n вершинами, имеющими вершину степени n-2.
Зафиксируем номер этой вершины. Тогда в коде Прюфера она встречается n-3 раз. Тогда для остальных n-1 вершин остается n-2-(n-3)=1 место. Кол-во выбора номера вершины степени n-2 из n равно n. Тогда искомое число деревьев равно 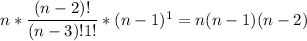
То есть, клиенту нужно: автомобиль на 2 дня на расстояние 800 км и топливо.
1 вариант:
Аренда автомобиля: 3 500 * 2 = 7 000 руб.
Топливо: 5 * 8 = 50 л на 800 км, а значит стоимость - 50 * 38 = 1 900 руб.
В итоге за 1 автомобиль нужно заплатить: 7 000 + 1 900 = 8 900 руб.
2 вариант:
Аренда: 2 700 * 2 = 5 400 руб.
Топливо: 6 * 8 = 48 л на 800 км, стоимость - 48 * 42 = 2 016 руб.
За 2 автомобиль нужно заплатить: 5 400 + 2 016 = 7 416 руб.
3 вариант:
Аренда: 2 800 * 2 = 5 600 руб.
Топливо: 8 * 8 = 64 л на 800 км, стоимость - 64 * 20 = 1 280 руб.
Стоимость 3 варианта: 5 600 + 1 280 = 6 880 руб.
Самый дешевый 3 вариант, а значит ответ: 6 880 рублей.