![\int \frac{dx}{sinx+cosx}=[\, t=tg\frac{x}{2},sinx=\frac{2t}{1+t^2},cosx=\frac{1-t^2}{1+t^2},dx=\frac{2dt}{1+t^2}\, ]=\\\\=\int \frac{\frac{2dt}{1+t^2}}{\frac{2t}{1+t^2}+\frac{1-t^2}{1+t^2}}=\int \frac{2\, dt}{-(t^2-2t-1)}=-2\int \frac{dt}{(t-1)^2-2}=[v=t-1,dv=dt]=\\\\=-2\int \frac{dv}{v^2-2}=-2\cdot \frac{1}{2\sqrt2}\cdot ln|\frac{v-\sqrt2}{v+\sqrt2}|+C=-\frac{1}{\sqrt2}\cdot ln|\frac{tg\frac{x}{2}-1-\sqrt2}{tg\frac{x}{2}-1+\sqrt2}|+C=](/tpl/images/0325/7226/86b12.png)

Пошаговое объяснение:
Разобьём всех гномов по тройкам, чтобы найти сколько из них могут стоять между гномами в колпаках одного цвета:
105:3=35, а нужно 67. Значит надо добавить к 32 тройкам по гному в таком же колпаке. Получается 32 квартета одного цвета и 3 тройки:
3×3+32×4=137.
31 гном лишний, т. е. 8 квартетов подряд должны быть одного цвета. Остаётся 16 квартетов и 3 тройки, из которых две соседние тройки должны быть одного цвета. Итак имеем 8 соседних квартетов одного цвета, 2 соседних тройки одного цвета, а также 16 квартетов и тройка разных цветов. Или всего имеем 27 наборов разных цветов. Если разместить их по кругу, то первый и последний наборы должны быть разных цветов. То есть красных наборов может быть (27-1):2=13. С каждой стороны красных наборов будут не красные наборы. Таким образом максимум 26 гномов в красных колпаках могут иметь соседа не в красном колпаке.
Задачу можно интерпретировать как 250 опытов с фиксированной вероятностью успеха и неудачи в каждом отдельном испытании, т.е. по факту мы имеем биномиальное распределение, применима формула Бернулли
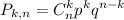
или в нашем случае
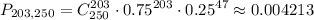
Если мощного калькулятора под рукой нет, то лучше вместо биномиального использовать нормальное распределение. Это допустимо, ведь из центральной предельной теоремы следует что при неограниченном возрастании числа опытов ф-я распределения будет неограниченно приближаться к нормальному распределению (с мат. ожиданием 0 и дисперсией 1)