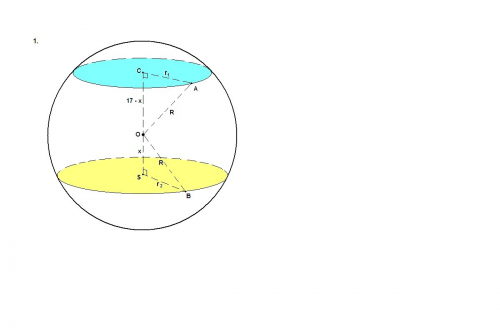
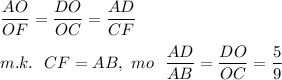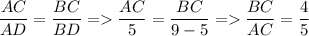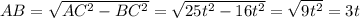Математика: Что находится в глазках у котофеля? ну у кортошки

Чертеж во вложении. 1. Проведем через вершину С прямую, параллельную катету АВ. Пусть F - точка пересечения этой прямой с продолжением медианы АМ за точку М. 2. ∆АДО и ∆ОСF подобны по двум углам (отмечены дугами). Отсюда равенство: По свойству биссектрисы внутреннего угла треугольника Пусть t - коэффициент пропорциональности. АС=5t, BC=4t. По теореме Пифагора в ∆АВС Отсюда следует, что стороны ∆АВС относятся как АВ:ВС:АС=3:4:5. Обозначим теперь ∠DCB=a (альфа), тогда cos ∠ACB = cos 2a = BC/AC=4/5....

Что находится в глазках у котофеля? ну у кортошки

👇

Увидеть ответ

Ответ:

Daria20081

19.09.2020

Клубни картофеля - это подземные стебли, а в их глазках почки.

4,4(41 оценок)

Открыть все ответы

Ответ:

marystuart21

19.09.2020

1. Сечение шара - круг. Площадь круга: S = πr².

S₁ = πr₁² = 25π ⇒ r₁ = 5

S₂ = πr₂² = 144π ⇒ r₂ = 12

Отрезок, соединяющий центр шара с центром сечения, перпендикулярен сечению.

Обозначим ОС = х, тогда OS = 17 - х.

Из прямоугольных треугольников ОСА и OSB выразим радиус шара по теореме Пифагора:

R² = (17 - x)² + r₁² = (17 - x)² + 25

R² = x² + r₂² = x² + 144

(17 - x)² + 25 = x² + 144

289 - 34x + x² + 25 = x² + 144

34x = 170

x = 5

R = √(x² + 144) = √(25 + 144) = √169 = 13

Sпов. шара = 4πR² = 4 · π · 169 = 676π

2. Так как вершины квадрата лежат на сфере, то квадрат вписан в сечение сферы, в окружность, центр которой лежит в точке пересечения диагоналей квадрата.

Отрезок, соединяющий центр сферы с центром сечения, перпендикулярен сечению. Тогда SD - проекция наклонной OD на плоскость АВС, значит ∠SDO = 60° - угол между радиусом и плоскостью АВС.

OS - искомое расстояние.

BD = 12√2 как диагональ квадрата,

SD = 6√2.

Из прямоугольного треугольника SOD:

tg 60° = SO / SD

SO = SD · tg 60° = 6√2 · √3 = 6√6

3. Так как стороны треугольника касаются шара, то круг - сечение шара - вписан в треугольник.

Отрезок, соединяющий центр шара с центром сечения, перпендикулярен сечению.

OS = √2 - расстояние от центра шара до плоскости треугольника.

Полупериметр треугольника АВС:

p = (8 + 10 + 12)/2 = 15

По формуле Герона:

Sabc = √(p·(p - AB)·(p - BC)·(p - AC))

Sabc = √(15 · 7 · 5 · 3) = √(5 · 3 · 7 · 5 · 3) = 15√7

Sabc = p·r, где r = SK - радиус вписанной окружности.

p · SK = 15√7

SK = 15√7 / 15 = √7

Из прямоугольного треугольника SOK по теореме Пифагора:

ОК = √(SK² + OS²) = √(7 + 2) = √9 = 3

R = 3

4. Ядро - шар. Если его переплавили в конус, значит объем шара и конуса одинаков.

Пусть R = 1 - радиус шара, r - радиус конуса.

Vшара = 4/3 π R³ = 4/3π

Vконуса = 1/3 πr² · h = 4/3π, отсюда

r² · h = 4

Из прямоугольного треугольника, образованного высотой, радиусом основания и образующей конуса, по теореме Пифагора:

r² + h² = 6

Получили систему уравнений:

r² · h = 4

r² + h² = 6

r² = 6 - h²

(6 - h²) · h = 4 (2)

Решим второе:

6h - h³ = 4

h³ - 6h + 4 = 0

(h - 2)(h² + 2h - 2) = 0

h = 2

или

h² + 2h - 2 = 0

D/4 = 1 + 2 = 3

h = - 1 - √3 - не подходит по смыслу задачи, или

h = - 1 + √3 - не подходит по условию, так как высота не меньше 1.

ответ: h = 2

1.сечения шара двумя параллельными плоскостями,между которыми лежит центр шара,имеют площади 144 пи

4,4(23 оценок)

Ответ:

anastasiyakorc

19.09.2020

Чертеж во вложении.
1. Проведем через вершину С прямую, параллельную катету АВ. Пусть F - точка пересечения этой прямой с продолжением медианы АМ за точку М.
2. ∆АДО и ∆ОСF подобны по двум углам (отмечены дугами). Отсюда равенство:
$\dfrac{AO}{OF}=\dfrac{DO}{OC}=\dfrac{AD}{CF}\\\\ m.k.\ \ CF=AB,\ mo\ \ \dfrac{AD}{AB}=\dfrac{DO}{OC}=\dfrac{5}{9}$
По свойству биссектрисы внутреннего угла треугольника
$\dfrac{AC}{AD}=\dfrac{BC}{BD} = \dfrac{AC}{5}=\dfrac{BC}{9-5}=\dfrac{BC}{AC}=\dfrac{4}{5}$
Пусть t - коэффициент пропорциональности. АС=5t, BC=4t.
По теореме Пифагора в ∆АВС
$AB=\sqrt{AC^2-BC^2}=\sqrt{25t^2-16t^2}=\sqrt{9t^2}=3t$
Отсюда следует, что стороны ∆АВС относятся как АВ:ВС:АС=3:4:5.
Обозначим теперь ∠DCB=a (альфа), тогда cos ∠ACB = cos 2a = BC/AC=4/5.
Из тригонометрических формул получим
$cos\ \alpha=\sqrt{\frac{1+cos\ 2\alpha}{2}}=\sqrt{\frac{1+\frac{4}{5}}{2}}=\sqrt{\frac{9}{10}}=\frac{3}{\sqrt{10}}$
Имеет место формула биссектрисы через стороны треугольника:
$DC=\dfrac{2BC*AC}{BC+AC}cos \frac{\angle ACB}{2}= \dfrac{2*4t*5t}{4t+5t}*\dfrac{3}{\sqrt{10}} \\ \dfrac{120t^2}{9t}*\dfrac{3}{\sqrt{10}} =14\\ t^2=\dfrac{21^2}{40}\\ S_{ABC}=\frac{1}{2}*3t*4t=6t^2=6*\frac{21^2}{40}=\frac{1323}{20}\\\\ Ombem: \frac{1323}{20}$
Медиана am и биссектриса cd прямоугольного треугольника abc угол b=90 пересекаются в точке o. найдит