ответ:
удастся помешать
пошаговое объяснение:
при выборе произвольного числа n и последующем действии в итоге могут быть получены числа n-1 или n+1, так как они отличаются на 2, а целью собаки является получить число кратное 4, то свинья любое произвольное единичное число может превратить в не кратное 4.
минимальное число чисел которое может задать собака для получения числа кратного 4 является два. это должны быть числа 4*z1 - 1 и 4*z2 + 1 (где z1 и z2 - целые числа). в этом случае как при увеличении, так и при уменьшении на 1, одно из чисел становится кратным 4.
в любой последовательности чисел с четным количеством членов не более половины может быть после действия свиньи кратным 4 (если свинья не поддается), в случае нечетного количества членов, свинья может выбрать действие, которое превращает в не кратные 4 больше половины членов ряда (можно разделить ряд на пары + 1 число и потом произвести над ними одно и то же действие так, что не более одного числа в паре станет кратным 4, а единичное число не будет кратно 4).
в итоге из произвольного ряда чисел (после действия свиньи) кратных 4 может быть получено не более n/2 для рядов с четным количеством членов и не более (n-1)/2 для рядов с нечетным количеством членов
таким образом максимальное количество чисел, кратных 4, которые может получить собака будет равно (2019-1)/2 = 1009
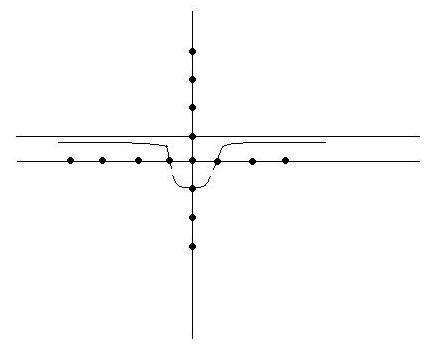
1) ОДЗ: x^2+1#0 - при любом х условие соблюдается. Т.е. функция непрерывная, определена на всей числовой оси.
2) Точки эксремума, промежутки возрастания и убывания ф-ции:
[(x^2-1)/(x^2+1) ]' = (2x*(x^2+1) - (x^2-1)*2x)/(x^2+1)^2 = (2x*( x^2+1-x^2+1))/ (x^2+1)^2=4x/ (x^2+1)^2 = 0, x=0.
x=0 - производная при переходе через эту точку меняет свой знак с минуса на плюс. Значит, это точка минимума. (0; -1) - минимум функции.
При x<0 - функция убывает, при x>0 - возрастает.
3) Нули функции: x=1, x= -1 - в этих точках график функции пересекает ось Ох. (1;0) и (-1;0).
4) В точке y=-1 график функции пересекает ось Оу. (0;-1)
5) Функция четная, симметричная относительно оси Оу.
6) Предел функции при х стремящимся к +бесконечности/-бесконечности равен 1. Значит, график будет приближаться к прямой у=1.
График прикрепляю - очень схематично. Поэтапно отмечаются точки, направления.