ответ: Чтобы обозначить числами точное положение точки на плоскости,
проводят две перпендикулярные координатные прямые — x и y ,
которые пересекаются в начале отсчета — точке О (смотри рисунок).
Эти прямые называют системой координат на плоскости, а точку О —
началом координат. Плоскость, на которой выбрана система координат,
называют координатной плоскостью.
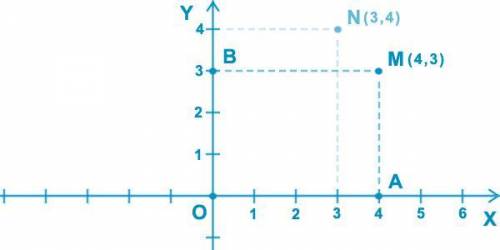
Пошаговое объяснение: Пусть M — некоторая точка плоскости. Проведем через нее прямую MA ,
перпендикулярную координатной прямой X , и прямую MB ,
перпендикулярную координатной прямой Y . Так как точка A имеет
координату 4, а точка B координату 3 , то положение точки M определяется
парой чисел (4, 3) . Эту пару чисел называют координатами точки M .
Число 4 называют абсциссой точки M , а число 3 — ординатой точки M .
Координатную прямую X называют осью абсцисс,
а координатную прямую Y — осью ординат.
Точку M с абсциссой 4 и ординатой 3 обозначают так: M (4, 3) .
На первом месте пишут абсциссу точки, а на втором ее ординату.
Если переставить координаты местами, то получится другая точка
N (3, 4) , которая тоже изображена на рисунке.
Каждой точке на координатной плоскости соответствует пара чисел: ее абсцисса и ордината, и наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
Пошаговое объяснение:
Вводим в рассмотрение события –гипотезы:
Н1–''выбрана винтовка с оптическим прицелом''
Н2–''выбрана винтовка без оптического прицела''
р(Н1)=3/10=0,3
р(H2)=7/10=0,7
Cобытие А – '' стрелок поразит мишень''
По условию вероятность события А при выстреле из винтовки с оптическим прицелом, равна 0,85;
p(A/H1)=0,85
Вероятность события А при выстреле из винтовки без оптического прицела эта вероятность равна 0,7
p(A/H2)=0,7
По формуле полной вероятности
р(А)=р(Н1)·р(А/Н1)+р(Н2)·р(А/Н2)=
=0,3·0,85+0,7·0,7=
=0,255+0,49=0,745
p(Н1/А)·р(А)=р(Н1)·р(А/Н1) ⇒
p(Н1/А)=0,255/0,745 ≈ 0,34
и
p(Н2/А)=0,49/0,745 ≈ 0,66
вероятнее, что стрелок стрелял из винтовки без оптического прицела
1) у'=3х²-8х+1
2) у'=28х³+2
3) у'=cosx+1/x