1) x≤2
2)x>3
3)2<x<12
Пошаговое объяснение:
1)
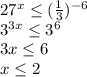
2)
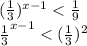
меняем знак, т.к. основание 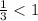

3)
опять будем менять знак, т.к. основание логарифма 1/3 < 1
свойства алгоритма применяемые в данном примере:
1)log(a)+log(b)=log(a*b)
2)a>0 и b>0
ОДЗ:
x-2>0 ----> x>2
12-x>0 ----> x<12

найдём дискриминант квадратного уравнения:
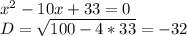
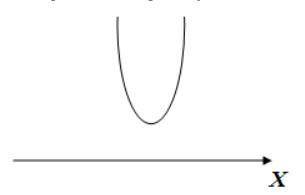
то, что дискриминант отрицательный нам говорит, что парабола не касается оси Ох, и т.к. коэффициент при x² >0, то ветви параболы направлены вверх(видно на рисунке), исходя из этого делаем выводы что данное квадратное уравнение положительно при любых х.
Включая ОДЗ, получаем ответ:
2<x<12(или x∈(2;12))
6 + 2√3
Пошаговое объяснение:
1) Площадь треугольника равна половине произведения его сторон на синус угла между ними:
S авс = (АВ · АС · sin∠А) : 2 = 2√3 · 4 · 0,5 : 2 = 2√3
2) С другой стороны, площадь ΔАВС равна половине произведения основания АС на высоту, опущенную из вершины В на сторону АС (назовём эту высоту ВF):
S авс = АС · BF : 2
Подставим вместо S авс её значение и найдём BF:
2√3 = АС · BF : 2
2√3 = 4 · BF : 2
BF = 2√3 : 2 = √3
3) Зная BF, найдём АF и FC.
AF = √(АВ² - BF²) = √((2√3)² - (√3)²) = √(4·3 - 3) = √9 = 3 см
FC = АС - АF = 4 - 3 = 1 см
4) Зная FC, найдём ВС по теореме Пифагора, т.к. Δ BFC - прямоугольный:
ВС = √(BF² + FC²) = √((√3)² + 1²) = √(3+1) = 2
5) Равс = АВ + ВС + АС = 2√3 + 2 + 4 = 6 + 2√3 = 2· (3 +√3)
2 переместительное
3 множители, произведение
4 числитель
5 больше