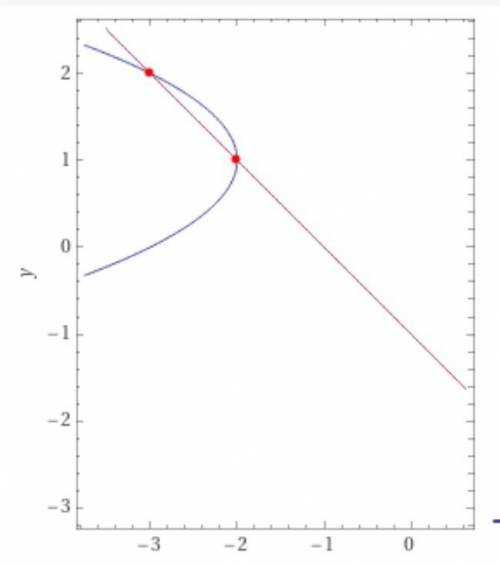
Даны уравнения кривой х + у ²- 2у + 3 = 0 и прямой х + у + 1 = 0.
1) В уравнении кривой выделяем полные квадраты:
(y²-2·1y + 1) -1·1 = (y-1)²-1 .
Преобразуем исходное уравнение:
(y-1)² = -x -2 .
Получили уравнение параболы:
(y - y0)² = 2p(x - x0) ,
(y-1)² = 2·(-1/2)(x - (-2)) .
Ветви параболы направлены влево, вершина расположена в точке (x0, y0), то есть в точке (-2;1) .
Параметр p = (-1/2 )
Координаты фокуса: F((xo + (p/2)); yo) = ((-2 - (1/4)); 1) =( (-9/4);1).
Уравнение директрисы: x = x0 - p/2
x = -2 - (-1/4) = (-7/4 ).
2) Координаты точек пересечения находим совместным решением уравнений кривой и прямой.
х + у ²- 2у + 3 = х + у + 1 ,
у ²- 3у + 2 = 0, Д = 9 - 4*1*2 = 1, у1 = (3 - 1)/2 = 1, у2 = (3 + 1)/2 = 2.
х1 = -у - 1 = -1 - 1 = -2, х2 = -2 - 1 = -3.
В правильной треугольной пирамиде центр описанного шара находится на высоте пирамиды в точке пересечения её срединным перпендикуляром к боковому ребру.
Также, тангенс угла β наклона бокового ребра к основанию в 2 раза меньше тангенса угла α наклона боковой грани к основанию.
Поэтому tg β = (1/2)*2√3 = √3.
sin β = tgβ /√(1 + tg²β) = √3/√(1 + 3) = √3/2.
Находим боковое ребро L.
Сначала находим высоту пирамиды H:
H = ((1/3)ho*tg α = (1/3)*3√3*2√3 = 6.
Тогда L = √(H² +((2/3)ho)²) = √(36 + (2√3)²) = √48 = 4√3.
Находим радиус R шара.
R = (L/2)/sin β = 2√3/(√3/2) = 4.
ответ:площадь поверхности шара равна 4πR² = 64π кв.ед.
4дм2см+9см6мм=420мм+96мм=516мм=5дм1см6мм
3м-2дм5мм=3000мм-205мм=2750мм=2м7дм5см
1км3м-89м=103м-89м=914м
5дм9см3мм+47мм=593мм+47мм=640мм=6дм4см