1. примеры, исходя из следующих условий. если цифры: а) имеет центральную симметрию, но не осевую симметрию; б) с осевой симметрией, но без центральной симметрии; в) есть центр и осевая симметрия. 2. abcd прямоугольные потолки на координатной плоскости соответственно (- 2; 2), (5; 3), (5; - 5), (- 1; 7). а) стена абсциссы с абсциссой; б) av стенка с осью ординат; в) ось ординаты сечения переменного тока; введите точку, в которой она пересечена. 3. даны точки m (-3; -4), n (-2; -5) и p (-6; -6). вставьте mnr треугольник. а) симметрично треугольнику mnr относительно оси абсцисс; б) треугольник mnr симметричен оси ординаты; (c) вставьте треугольники так, чтобы треугольник mnr был симметричен координатам головы. !
-----------
При делении меньшего числа на большее возможны два варианта: обыкновенная дробь или десятичная.
Запишем данные для деления числа в виде дроби. В числителе меньшее число, в знаменателе большее.
Получим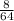 .
.
Если числитель и знаменатель составные числа и имеют общий делитель, их можно сократить. В данном случае сократим на 8, тогда дробь, имея то же значение, будет выглядеть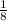 .
.
Можно сказать, что если делимое меньше делителя, то частное равно нулю, а остаток равен делимому.
8:64=0(ост.8)
-----------
Деление в столбик.
Слева записываем делимое, справа делитель так, как показано в приложении.
При делении меньшего числа на большее получим число меньше единицы. В результате под под чертой пишем 0 и ставим запятую.
0 умножаем на 64, получим 0 - записываем под делимым, вычитаем. Под чертой получим остаток 8. Приписываем к нему 0 - получим число 80. Это число уже больше 64 . Производим деление - после запятой под делителем подбираем нужное число ( здесь пишем 1). Умножим 1 на 64, запишем под 80 и вычтем. В остатке получим 16. Дописываем 0, к числу под делителем дописываем 2 и умножаем на делитель.
Продолжаем. Если в результате действий при вычитании получим 0, - отлично. Если нет - у нас получится бесконечная десятичная дробь, что тоже является результатом.
----------
Вариант №3 - воспользоваться калькулятором.