x^2-6x+y-1=0
y = 1+6x-x^2
В первом ящике было 119 карандашей, а во втором - 17.
Пошаговое объяснение:
Пусть во втором ящике будет х карандашей, тогда в первом будет 7 * х карандашей.
Когда из первого ящика взяли 38 карандашей, запишем так:
(7 * х - 38) карандашей осталось в первом ящике.
Когда со второго ящика взяли 14 карандашей, запишем так:
(х - 14) карандашей осталось во втором ящике.
Во втором ящике осталось на 78 карандашей меньше, значит если от первого ящика вычесть второй, получим 78. Запишем в виде уравнения:
(7х - 38) - (х - 14) = 78;
7х - х - 38 + 14 = 78;
6х = 78 + 38 - 14;
6х = 102;
х = 17.
7х = 7 * 17 = 119.
ответ: в первом ящике было 119 карандашей, а во втором - 17.
частное x³ + 2x² + 6x + 2, остаток 5
Пошаговое объяснение:
x⁴ + 2x² - 10x + 1 разделить на x - 2 по схеме Горнера:
В нашем случае x - a = x - 2, а значит a = 2. Обращаем внимание на то, что коэффициент при x³ равен 0
Выписываем в строчку a за ним коэффициенты многочлена
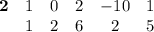
Под старшим коэффициентом пишем его же (в нашем случае 1), умножаем написанное на a (у нас 2) прибавляем к следующему коэффициенту (у нас 0). Результат записываем в следующую позицию второй строчки (1 · 2 + 0 = 2). С записанным числом повторяем те же действия (2 · 2 + 2 = 6), и так далее...
Получили частное x³ + 2x² + 6x + 2, остаток 5
Выделяем полные квадраты:
(x²-2*3x + 3²) -3² = (x-3)²-9
Преобразуем исходное уравнение:
(x-3)² = -y + 10
Получили уравнение параболы:
(x - x0)² = 2p(y - y0)
(x-3)² = 2(-1/2)(y - 10)
Ветви параболы направлены вниз (p<0), вершина расположена в точке (x0, y0), т.е. в точке (3;10)
Параметр p = -1/2
Координаты фокуса: F(xo; P/2) = (3; ((1/2)/2)).
Уравнение директрисы: y = y0 - p/2
y = 10 - (-1/4) = 41/4.