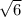
Пошаговое объяснение:
Расстояние между двумя числами на числовой оси — просто модуль их разности. Получим, чему оно равно, не решая самого уравнения: его корни выглядят не очень красиво, к тому же получается 4 пары корней.
Возведём первое уравнение в квадрат:
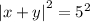
Знак модуля можно поменять на обычные скобки: возведение в квадрат "съест" все минусы, если такие будут
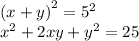
Вычтем из левой и правой части уравнения 4xy. Поскольку xy = 4,75, то 4xy = 19:
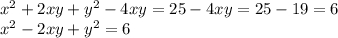
В левой части стоит в точности квадрат разности. Значит, будет просто извлечь квадрат (корень из a² — модуль a):
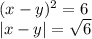
координаты фокусов: 
длина осей : действительная ось 12; мнимая ось 10
эксцентриситет: 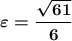
Пошаговое объяснение:
Каноническое уравнение гиперболы имеет вид
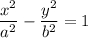
Приведем наше уравнение к каноническому виду.
900 переносим в правую часть и одновременно делим все части уравнения на 900.
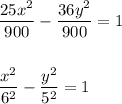
Таким образом, мы получили каноническое уравнение гииперболы с центром в точке С(0; 0).
а = 6; b = 5
Действительная ось 2а = 12.
Мнимая ось 2b = 10
Расстояние от центра симметрии до каждого из фокусов рассчитывается по формуле: 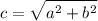 .
.
Фокусы имеют координаты F₁ (-c; 0) ; F₂(c; 0).
Найдем фокусы нашей гиперболы.
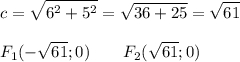
Эксцентриситетом гиперболы это отношение
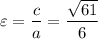
#SPJ1
504:21=24(км/ч) --- скорость теплохода против течения
24+2=26(км/ч) --- скорость теплохода в стоячей воде
26+2=28(км/ч) --- скорость теплохода по течению
504:28=18(ч) --- ответ