S(пол) = S(осн)+S(бок) .
Если боковые грани наклонены к плоскости основания под одинаковым углом (в данном случае α), то высота пирамиды проходит через центр окружности вписанной в основании.
S(осн) =b*b*sinβ =b²sinβ.
С другой стороны S(осн) =p*r =(4b/2)*r =2b*r⇒r =b²sinβ/2b = bsinβ/2.(Это можно было написать сразу).
S(бок) =4*b*h/2=2bh , где h апофема боковой грани.
r =h*cosα ⇒h =r/cosα = (bsinβ/2)/cosα =bsinβ/(2cosα) .
Следовательно: S(бок)=2bh=2b*(bsinβ/(2cosα)) = b²sinβ/sinα (И это можно было написать сразу).
Окончательно :
S(пол) = b²sinβ+ b²sinβ/sinα =b²sinβ(1+ 1/sinα)=b²(sinβ/sinα)*(1+ sinα).
ответ: b²(sinβ/sinα)*(1+ sinα).
1+sinα = 1+cos(π/2 -α) =2cos²(π/4 -α/2).
1+sinα =sinπ/2 +sinα =...
Изучаемый прямоугольный треугольник имеет катеты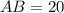 
и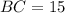 
и гипотенузу 
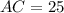(чертеж в приложении).
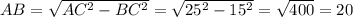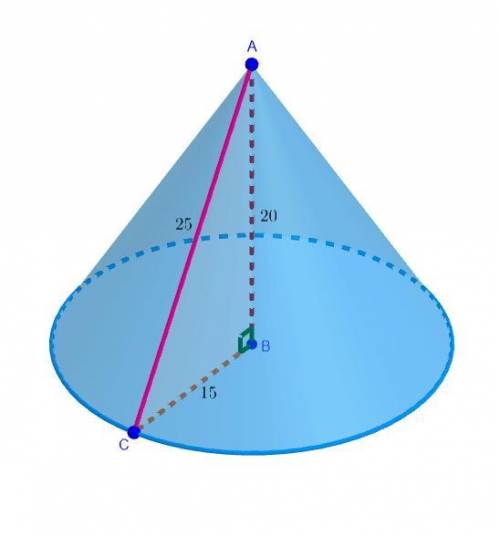
.Из этого следует, что вращали треугольник вокруг катета, равного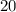 
(это есть больший катет, 
).
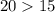При вращении прямоугольного треугольника вокруг одного из катетов, как известно, получается конус. В данном случае его высота равна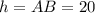 
, радиус основания 
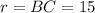и образующая 
.
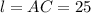Для вычисления полной поверхности конуса используем соответствующую формулу:
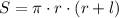
Подставляем известные значения:
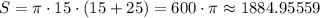
ответ: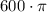 
или около 
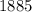(ед³).
