Пошаговое объяснение:
lnx+lny=xy
1) y'
дифференцируем обе части
(lnx+lny)'=(xy)'
(1/x)+(1/y)=x'y+y'x
(1/x)+(1/y)=y+y'x (1) используем это равенство при нахождении y''
y'x=(1/x)+(1/y)-y
y'=[(1/x)+(1/y)-y]/x
y'=(1/x²)+(1/(xy))-(y/x) (2) используем это равенство при нахождении y''
2) y''
(1/x)+(1/y)=y+y'x (1)
((1/x)+(1/y))'=(y+y'x)'
((-1/x²)+(-y'/y²)=y'+y''x+y'
((-1/x²)+(-y'/y²)=2y'+y''x
y''x= ((-1/x²)+(-y'/y²)-2y'
y''= [((-1/x²)+(-y'/y²)-2y']/x
y''= ((-1/x³)+(-y'/xy²)-2y'/x
y''= ((-1/x³)-y'[(1/xy²)+(2/x)] подставим сюда y'=(1/x²)+(1/(xy))-(y/x) (2)
y''= ((-1/x³)-[(1/x²)+(1/(xy))-(y/x)]{(1/xy²)+(2/x)}
.
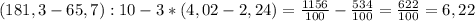Пошаговое объяснение:
Нам дано выражение:
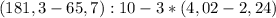
В длинных выражениях с различными знаками вычитания, сложения, умножения и деления, первым делом упрощается то, что находится в скобках.
1- Поэтому первым действием будет вычитание в левой скобке:
2 - Преобразуем правую скобку по такому же принципу:
3 -Теперь вернёмся в левую часть выражения и поделим получившуюся разность в скобке 115,6 на 10: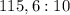
.
Представим данное выражение в виде двух дробей: 115,6 переведем в неправильную дробь, где получим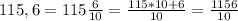 
, а число десять представим в виде дроби 
. Теперь запишем данное деление в ином виде:
При делении двух дробей, вторая "переворачивается" и происходит их умножение:
4 -Теперь итог правой дроби умножим на 3:
Получили две неправильные дроби с одинаковым знаменателем.
5 - Теперь мы легко можем вычесть из первой дроби вторую:
.
log10x=3 log10X=-4 x=2
x=10^3 X=10^-4
x=1000 x=1/10000
ну как-то так
log32x=-4/5 log0.01x=-3/2
x=2^-4 x=0.5^3
x=1/16 x=0.125
все))
41.13
в) logx49=2 г)logx8=-1/3
x=7 x=5