Найдем сначала общее решение соответствующего однородного дифференциального уравнения
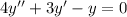
Пусть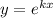 
, мы получим характеристическое уравнение
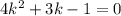
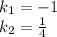
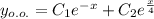— общее решение однородного диф. ур.
Найдём теперь частное решение. Рассмотрим функцию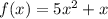 
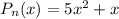отсюда 
; 
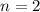. Сравнивая 
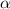с корнями характеристического уравнения и, принимая во внимая, что , частное решение будем искать в виде:
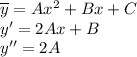
Подставляем в исходное дифференциальное уравнение
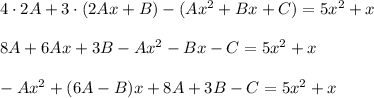
Приравниваем коэффициенты при степени x
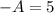откуда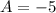 
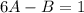откуда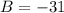 
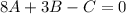откуда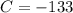 
Частное решение: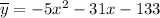 
Общее решение линейного неоднородного дифференциального уравнения:
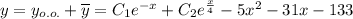
Задача № 1
Предположим, что в классе х (%) девочек, тогда мальчиков в классе (х+20) %, также примем во внимание, что всего в классе 100% учеников
согласно этим данным составим и решим уравнение:
х+х+20=100
2х+20=100
2х=100-20
2х=80
х=80:2
х=40 (%) - учеников в классе составляют девочки.
40+20=60 (%) - учеников в классе составляют мальчики.
ответ: мальчики составляют 60% учащихся класса, а девочки - 40%
Проверка:
40+60=100 (%) - всего учащихся в классе.
Задача № 2
составим пропорцию:
8% -100%
х% - 25%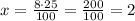
(%)
ответ: молоко содержит 2% жира.
2)45-20=25(н)
ответ:25 наклеек у Светы