Пошаговое объяснение:
Задача на комбинаторику.
В комбинаторике разделяют два типа задач: на сочетания и размещения.
Сочетание - это тип задач в комбинаторике, в которых порядок элементов не важен.
Размещение - это тип задач в комбинаторике, в которых порядок элементов важен.
У нас задача на размещение.
Формула для решения задач на размещения:
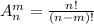
Где n - общее количество карт в колоде; m - количество вальтов; дам.
Подставляем значения в формулу:
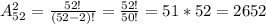
Напоминаю, что 52! это - 1 * 2 * 3 * 4 * 5 * 6 ... * 52.
Следовательно, 50! это - 1 * 2 * 3 * 4 * 5 * 6 ... * 50
52! и 50! можем сократить на 50!, в числителе останется 51 * 52, а в знаменателе - 1(мы числитель и знаменатель всегда можем домножить на единицу).
Получаем
Решаем пункт б:
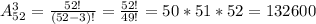
Все то же самое, что и в пункте а.
Задача решена.
тагда раз там 3х,a не 3k будет такое уравнение
z=3x+2y
x = 1 + 2 + 3 + 6 + 7 - 8y=19-8y
z=x-x/7=(7x-x)/7=6x/7
(6*(19-8y)/7=3*(19-8y)+2y
(114-48y)/7=57-24y+2y
(114-48y)/7=57-22y
114-48y=7(57-22y)
114-48y=399-154y
-48y+154y=399-114
106y=285
y= 2 73/106
проверка:
6x/7=3x+2y
6x=7(3x+2y)
6x=21x+14y
6(19-8*2 73/106)=21(19-8*2 73/106)+14(2 73/106)
19-8*285/106=19-21 54/106=-2 54/106=-2 27/53
6*(-2 27/53)=-6*133/53=-798/53=-15 3/53
21*(-133/53)=-52 37/53
14*285/106=3990/106=37 68/106=37 34/53
-52 37/53+37 34/53=-15 3/53
-15 3/53=-15 3/53
2) 4347/0,27=16100
3)119/476=0,25
4)10+4 - всего взяли красок
248 / 10/(10+4)=347.2 взято всего
347,2 * 4/(10+4)=99,2
ответ:99,2