Длины сторон параллелограмма:
АВ = CD = 3 см; ВС = AD = 9 см
Пошаговое объяснение:
Требуется найти стороны параллелограмма.
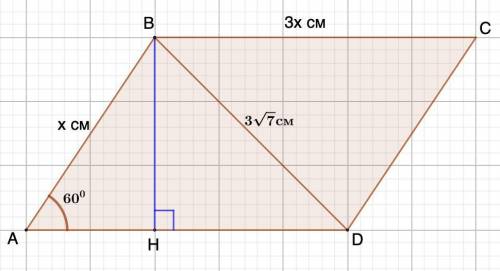
Для того, чтобы решить задачу, сделаем чертеж.
Из вершины В опустим высоту на AD.
Дано: ABCD - параллелограмм;
ВС : АВ = 3;
BD = 3√7 см; ∠А = 60°.
Найти: AB; BC; CD; AD.
1. По условию: ВС : АВ = 3.
Пусть АВ = х см, тогда ВС = 3х см.
Противоположные стороны параллелограмма равны.⇒ АВ = CD = x см; ВС = AD = 3x см.
2. Рассмотрим ΔАВН - прямоугольный.
∠А = 60° (по условию)
Сумма острых углов прямоугольного треугольника равна 90°.⇒ ∠АВН = 90° - 60° = 30°
Катет, лежащий против угла в 30°, равен половине гипотенузы.⇒ 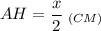
По теореме Пифагора:
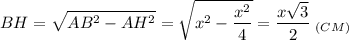
3. Рассмотрим ΔHBD - прямоугольный.
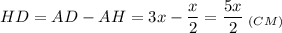
По теореме Пифагора:
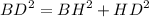
Подставим значения и решим уравнение:
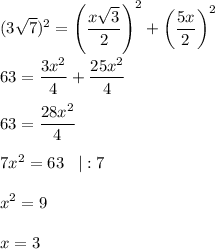
Стороны АВ = CD = 3 см.
Найдем ВС:
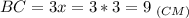
Стороны ВС = AD = 9 см.
(4/5 - 11/15) х 5/11 =((4*3-11)/15)*5/11=
=1/15*5/11=1/33
2) 7/88 × (8 / 21+ 8/7) =7/88*(8*2+8*6)/42=
=7/88*(16+48)/42=
=7/88*64/42=32/264=17/132
3) 3/7×(1/4+7/12)=3/7*(1*3+7)/12=3/7*10/12=10/28=5/14