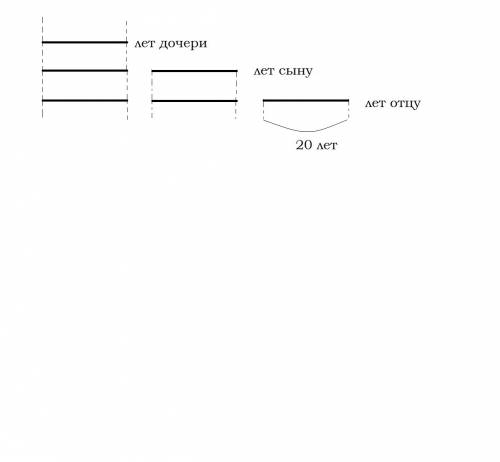
в приложении схема)
----------- лет дочери ( 1 часть)
----------- ----------- лет сыну ( 1 * 2 = 2 части - вдвое старше)
----------- ----------- ---------- лет отцу ( 1 + 2 = 3 части, возраст сына + возр. дочери)
_20 лет__
по схеме видим: 1 часть = 20 лет
3 - 2 = 1 часть - на столько сын моложе отца
1 часть = 20 лет - возраст дочери
20 * 2 = 40 лет - возраст сына
20 * 3 = 60 лет возраст отца
ответ: 20 лет, 40 лет, 60 лет.
проверка: 40 : 20 = 2 раза сын старше сестры - верно. 20 + 40 = 60 лет - вместе сыну и дочери, 60 = 60 - верно.
пусть возраст дочери х лет
2х лет - возраст сына
х + 2х лет - возраст отца и
2х + 20 лет - возраст отца
составляем уравнение:
х + 2х = 2х + 20
х + 2х - 2х = 20
х = 20 лет - возраст дочери
20 * 2 = 40 лет - возраст сына
20 * 3 = 60 лет - возраст отца
ответ: 20 лет, 40 лет, 60 лет.
Відповідь:
Покрокове пояснення:
Cоставляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r^2 -3 r + 2 = 0
D=(-3)^2 - 4·1·2=1
Корни характеристического уравнения:
r1 = 2
r2 = 1
Следовательно, фундаментальную систему решений составляют функции:
y1 = e^(2x)
y2 = e^x
Общее решение однородного уравнения имеет вид:
y- = C1*e^(2x) +C2*e^x, Ci ∈ R.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)) имеет решение
y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx)).
Здесь P(x) = 1, Q(x) = 0, α = 1, β = 0.
Следовательно, число α + βi = 1 + 0i является корнем характеристического уравнения кратности k = 1(r2).
Уравнение имеет частное решение вида:
y· = x (Ae^x)
Вычисляем производные:
y' = A·x·e^x+A·e^x
y'' = A(x+2)·e^x
которые подставляем в исходное дифференциальное уравнение:
y'' -3y' + 2y = (A(x+2)·e^x) -3(A·x·e^x+A·ex) + 2(x (Ae^x)) = e^x
или
-A·e^x = e^x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
1: -A = 1
Решая ее, находим:
A = -1;
Частное решение имеет вид:
y·=x (-1e^x)
Таким образом, общее решение дифференциального уравнения имеет вид:
y = y- + y. = C1*e^(2x) +C2*e^x - x *e^x.