На базу за три дня завезли 66 т овощей, причем во второй день завезли 60% количества овощей, завезенных в первый день, а в третий - 3/5 того, что было завезено в первый день. сколько овощей завезли в каждый из дней

👇

Ответ:

ШАТАНТРУБА

06.09.2021

Пусть х тонн завезли в первый день, тогда во второй день завезли 0.6х тонн и в третий день 3х/5 тонн. Зная что всего завезли 66 тонн, составим уравнение
х + 0.6х + 3х/5 = 66
1.6х + 0.6х = 66
2.2х = 66
х = 66/2.2
х = 30 тонн завезли в первый день
0.6 * 30 = 18 тонн завезли во второй день
3 * 30/5 = 18 тонн завезли в третий день

4,4(90 оценок)

Открыть все ответы

Ответ:

fearsomehusky

06.09.2021

(0;2]U[4;6)

Пошаговое объяснение:

ОДЗ:

{x > 0;

{6–x > 0 ⇒ x < 6

{(x4–12x3+36x2) > 0⇒ (x·(6–x))2 > 0 ⇒ x≠0; x≠6

ОДЗ: х∈(0;6)

при х∈(0;6):

log2(x4–12x3+36x2)=log2x2·(6–x)2=

log2(x·(6–x))2=2log2x·(6–x)=2log2x+2log2(6–x)

Неравенство принимает вид:

(2–log2x)·(log2(6–x)–2) ≥ 0

Применяем обобщенный метод интервалов

log2x=2 или log2(6–x)=2

x=4 или 6–х=4;х=2

При х=1

(2–log21)·(log2(6–1)–2)=2·(log25–log24) > 0

При х=3

(2–log23)·(log2(6–3)–2)=–(2–log23)2 < 0

При х=5

(2–log25)·(log2(6–5)–2)=(log24–log25)·(0–2) > 0

(0)__+__ [2]__–__[4]__+__ (6)

4,7(5 оценок)

Ответ:

nurayhasanova2oztngy

06.09.2021

Пошаговое объяснение:

сначала "отсечем" не нужное нам время. это время на 12 км по равнине - оно одинаково для пути и туда, и обратно

$\displaystyle t_1=\frac{S}{v} = \frac{12}{18} = \frac{2}{3}$ (часа)

теперь мы это время исключим из пути

туда (из А в В), заметим, что 1ч 7 мин = 67/60 мин

тогда время на прохождение з км в гору и потом 6 км под гору

будет

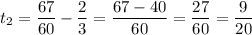$\displaystyle t_2=\frac{67}{60} -\frac{2}{3} =\frac{67-40}{60} = \frac{27}{60} =\frac{9}{20}$ (час)

а обратно, ((здесь заметим, что 1ч 16 мин = 76/60 мин) время на прохождение пути 6 км в гору и 3 км под гору будет

$\displaystyle t_3=\frac{76}{60} -\frac{2}{3} =\frac{76-40}{60} =\frac{36}{60} =\frac{3}{5}$

каждое из времен t₂ и t₃ складывается из времени в гору и времени под гору. только в одном случае путь в гору - это 3 км, а в другом - 6 км

обозначим скорость в гору х км/час

скорость под гору у км/час

если мы напишем уравнение для t₂ и t₃ через путь и скорость, то получим систему уравнений

t₂ - это 3 км со скоростью х км/час + 6км со скоростью у км/час

t₃ - это 6 км со скоростью х км/час + 3км со скоростью у км/час

$\displaystyle \left \{ {{\displaystyle\frac{3}{x}+\frac{6}{y}=\frac{9}{20} } \atop {\displaystyle\frac{3}{y} +\frac{6}{x} =\frac{3}{5} }} \right.$

теперь из второго найдем 3/у и подставим это в первое

$\displaystyle \frac{3}{y} = \frac{3}{5} -\frac{6}{x} \qquad \boldsymbol {(3)}\\\\\frac{3}{x} +\frac{6}{5} -\frac{12}{x} =\frac{9}{20} \\\\-\frac{9}{x} = \frac{9}{20} -\frac{6}{5} =\frac{9-24}{20} =-\frac{15}{20} =-\frac{3}{4} \\\\\underline {\boldsymbol {x=12}}$