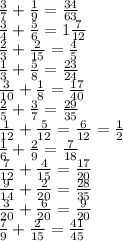
Работу по строительству дома примем за единицу (целое).
Пусть х дней - время работы первой бригады, (х + 5) дней - время работы второй бригады, тогда 1/х - часть дома, которую построит первая бригада за 1 день, 1/(х+5) - часть дома, которую построит вторая бригада за 1 день, 1/6 - часть дома, которую они построят вместе за 1 день. Уравнение:
1/х + 1/(х+5) = 1/6
Приводим обе части уравнения к общему знаменателю х · (х + 5) · 6
(х + 5) · 6 + х · 6 = х · (х + 5)
6х + 30 + 6х = х² + 5х
х² + 5х - 6х - 6х - 30 = 0
х² - 7х - 30 = 0
D = b² - 4ac = (-7)² - 4 · 1 · (-30) = 49 + 120 = 169
√D = √169 = 13
х₁ = (7-13)/(2·1) = (-6/2) = -3 (не подходит, так как < 0)
x₂ = (7+13)/(2·1) = 20/2 = 10 (дн.) - время работы первой бригады
ответ: С) 10.
Проверка:
10 + 5 = 15 дней - время работы второй бригады
1/10 + 1/15 = 3/30 + 2/30 = 5/30 = 1/6 - вместе за 1 день
1 : 1/6 = 1 · 6/1 = 6 дней - время строительства дома
5)5100
Пошаговое объяснение:
S = 100²-98²+96²-94²+...+4²-2²=
= (100²-98²) + (96²-94²) +...+ (4²-2²) =
= (100-98)*(100+98) + (96-94)*(96+94) + ... +
+ (4-2)*(4+2) =
= 2*(100+98) + 2*(96+94) + ... + 2*(4+2) =
= 2* (100+98+96+94+...+4+2) = 2 * S1,
где S1=(100+98+96+94+...+4+2) — сумма арифметической прогрессии с а(1)=100, a(n)=2 и d=98-100=-2.
Найдем n:
a(n)=a(1)+d*(n-1)
2=100+(-2)*(n-1)
2-100=(-2)*(n-1)
-98=(-2)*(n-1)
n-1=-98 : (-2)
n-1=49
n=49+1
n=50
тогда S1=Sn=(a(1)+a(n))*n/2=
=(100+2)*50/2=102*25=2550
Соответственно, S=2*S1=2*2550=5100