Сначала распишем все формулы и тогда будем вычислять пошагово.
Формула площади боковой поверхности: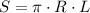 
Формула площади полной поверхности: 
Также формула площади полной поверхности: 
.
1) Площадь основания считается проще некуда, так как площадь полной поверхности - это сумма площади боковой поверхности и площади основания.
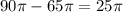cм².
2) Отсюда считаем радиус основания:
. Радиус основания конуса равен 5 см.
3) Вычисляем образующую:
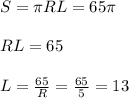cм. Образующая равна 13 см.
4) Высоту вычислить ещё проще. Конус образуется вращением прямоугольного треугольника вокруг его катета (высоты). Высоту можно было бы вычислить по теореме Пифагора, но в этом нет необходимости, так как в данном случае присутствует египетский треугольник с катетами 5 см и 12 см и гипотенузой 13 см (в данном случае гипотенуза это образующая). Высота равна 12 см.
5) Объём конуса вычисляется по формуле: 
В данном случае число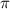 
мы трогать не будем, так как площади боковой и полной поверхностей представлены в форме с
см³.
АВСД- квадрат, по т. Пифагора диагональ АС=√(а²+а²)=а√2
ΔАКО: АК=а, АО=(а√2)/2
по т. Пифагора КО=√(а²-((а√2)/2)²=√а²/2=а/√2=(а√2)/2
сечение А₁В₁С₁Д₁. точка пересечения диагоналей сечения О₁.
по т. Пифагора А₁С₁=√(b²+b²)=b√2
ΔАКС: АС=а√2, АК=КС=а. прямая А₁С₁ отсекает от ΔАВС подобный ΔА₁КС₁
коэффициент подобия к=АС:А₁С₁, к=а√2:b√2, к=а:b
КО:О₁К=а:в, О₁К=(КО*в)/а, О₁К=(а*в√2)/а, О₁К=(b√2)/2
высота усеченной пирамиды: О₁О=КО-КО₁, О₁О=(а√2)/2-(b√2)/2, О₁О=(√2/2)*(а-b)
V=(1/3)*OO₁*(S₁+√S₁*S₂+S₂)
S₁=a², S₂=b²
V=(1/3)*(√2/2)*(a-b)*(a²+√a²b²+b²)
V=(√2/6)*(a-b)*(a²+ab+b²)
V=(√2/6)*(a³-b³)