ответ: (2, -1, 1)
Пошаговое объяснение: Запишем систему уравнений в матричном виде.
![\left[\begin{array}{cccc}3&-1&2&9\\2&3&-1&0\\2&4&3&3\end{array}\right]](/tpl/images/1055/0577/e1322.png)
Приведем к ступенчатому виду. Применяем операцию 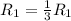 к
к  (к 1 строке) для того, чтобы сделать некоторые элементы строки равными 1.
(к 1 строке) для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\2&3&-1&0\\2&4&3&3\end{array}\right]](/tpl/images/1055/0577/6eddc.png)
Применяем операцию 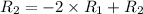 к
к  (ко 2 строке) для того, чтобы сделать некоторые элементы строки равными 0.
(ко 2 строке) для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\2&3&-1&0\\2&4&3&3\end{array}\right]](/tpl/images/1055/0577/6eddc.png)
Применяем операцию 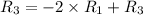 к
к  (к 3 строке) для того, чтобы сделать некоторые элементы строки равными 0.
(к 3 строке) для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\0&\frac{11}{3} &-\frac{7}{3}&-6 \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/0d2b8.png)
Применяем операцию 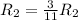 к
к  для того, чтобы сделать некоторые элементы строки равными 1.
для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\0&1&-\frac{7}{11} &-\frac{18}{11} \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/8a8f7.png)
Применяем операцию 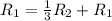 к
к  для того, чтобы сделать некоторые элементы равными 0.
для того, чтобы сделать некоторые элементы равными 0.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/c212b.png)
Применяем операцию  к
к  для того, чтобы сделать некоторые элементы строки равными 0.
для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&\frac{51}{11} &\frac{51}{11} \end{array}\right]](/tpl/images/1055/0577/960ac.png)
Применяем операцию 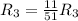 к
к  для того, чтобы сделать некоторые элементы строки равными 1.
для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&1 &1 \end{array}\right]](/tpl/images/1055/0577/ffa18.png)
Применяем операцию 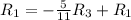 к
к  для того, чтобы сделать некоторые элементы строки равными 0.
для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&0&0&2 \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&1 &1 \end{array}\right]](/tpl/images/1055/0577/a5101.png)
Применяем операцию 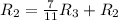 к
к  для того, чтобы сделать некоторые элементы равными 0.
для того, чтобы сделать некоторые элементы равными 0.
![\left[\begin{array}{cccc}1&0&0&2\\0&1&0&-1\\0&0&1&1\end{array}\right]](/tpl/images/1055/0577/927aa.png)
Воспользуемся полученной матрицей для того, чтобы описать итоговое решение системы уравнений.

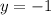
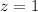
Решением является множество упорядоченных пар, которые удовлетворяют системе.
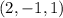
1.1 Учащийся приходит в школу за 15-20 минут до начала занятий, чистый и опрятный, снимает в гардеробе верхнюю одежду, занимает свое рабочее место и готовит все необходимые учебные принадлежности к предстоящему уроку.
1.2 Нельзя приносить в школу и на ее территорию с любой целью и использовать любым оружие, взрывчатые, взрыво- или огнеопасные вещества; спиртные напитки, наркотики, другие одурманивающие средства, а также токсичные вещества и яды.
1.3. Нельзя без разрешения педагогов уходить из школы и с ее территории в урочное время. В случае пропуска занятий учащийся должен предъявить классному руководителю справку от врача или записку от родителей (лиц, их заменяющих) о причине отсутствия на занятиях. Пропускать занятия без уважительных причин не разрешается.
1.4. Учащийся школы проявляет уважение к старшим, заботится о младших. Школьники уступают дорогу взрослым, мальчики (юноши) - девочкам (девушкам).
1.5. Вне школы учащиеся ведут себя везде и всюду так, чтобы не уронить свою честь и достоинство, не запятнать доброе имя школы.
1.6. Учащиеся берегут имущество школы, аккуратно относятся как к своему, так и к чужому имуществу.
Поведение на занятиях.
2.1. При входе педагога в класс учащиеся встают в знак приветствия и садятся после того, как педагог, ответив на приветствие, разрешит сесть. Подобным образом учащиеся приветствуют любого взрослого, вошедшего в класс во время занятий.
2.2. Во время урока нельзя шуметь, отвлекаться самому и отвлекать товарищей от занятий посторонними разговорами, играми и другими не относящимися к уроку делами. Урочное время должно использоваться учащимися только для учебных целей.
2.3. Если во время занятий учащемуся необходимо выйти из класса, то он должен поднять руку и попросить разрешения педагога.
2.4. Если учащийся хочет задать вопрос учителю или ответить на вопрос учителя, он поднимает руку.
2.5. Звонок (сигнал) об окончании урока дается для учителя. Только когда учитель объявит об окончании занятий, учащийся вправе покинуть класс. При выходе учителя или другого взрослого из класса учащиеся встают.
Поведение до начала, в перерывах и после окончания занятий.
3.1.Во время перерывов (перемен) учащийся обязан:
- навести чистоту и порядок на своем рабочем месте;
- выйти из класса;
- подчиняться требованиям педагога и работников школы;
подготовить класс по педагога к следующему уроку.
3.2. Учащимся запрещается:
- бегать по лестницам, вблизи оконных проемов и в других местах, не при для игр;
- толкать друг друга, бросаться предметами и применять физическую силу;
- употреблять непристойные выражения и жесты, шуметь, мешать отдыхать другим.
3.3. Дежурный по классу:
- находится в классе во время перемены;
- обеспечивает порядок в классе;
педагогу подготовить класс к следующему уроку;
- после окончания занятий производит посильную уборку класса.
3.4. Учащиеся, находясь в столовой:
- подчиняются требованиям педагога и работников столовой;
- соблюдают очередь при получении еды;
- проявляют внимание и осторожность при получении и употреблении горячих и жидких блюд;
- употребляют еду и напитки, приобретенные в столовой и принесенные с собой, только в столовой;
- убирают за собой посуду после принятия пищи.
Заключительные положения.
4.1. Учащиеся не имеют права во время нахождения на территории школы и при проведении школьных мероприятий совершать действия, опасные для жизни и здоровья самих себя и окружающих.
4.2. Настоящие правила распространяются на территорию школы и на все мероприятия, проводимые школой.