Пошаговое объяснение:
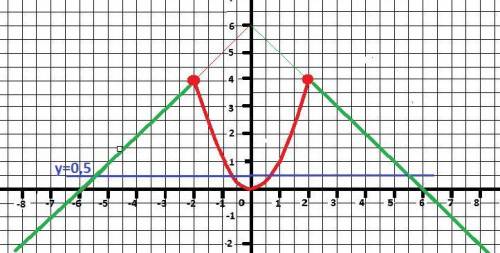
1) Рисунок с графиком функции в приложении.
2)
f(-2) = (-2)² = 4
f(0) = 0
f(1.25) = 1.5625
f(6) = 0
3)
D(f) = (-∞;+∞) - область определения функции
Максимальное значение при х = ± 2.
Ymax(2) = 4 - максимальное значение
E(f) = (-∞;4) - область значений функции.
4) Три варианта ответа.
а = 2 - два корня - х = ± 2.
0 < a < 2 - четыре корня.
а = 0 - три корня - х1 = -6, х2 = 0 и х3 = +6
5) Неравенства.
Три участка для равенства..
f(x) = 0.5.
x +6 = 0.5 x = - 5.5
-x +6 = 0.5 x = 5.5
x² = 0.5, x = ± √2 ≈ ± 0.7
Записываем решение неравенств.
f(x) > 0.5 x∈(-5.5;5.5)
f(x) <0.5 x∈(-∞;-5.5)∪(5.5;+∞)
Две последние цифры результата 21 в 2019 степени и 11 в 2020 степени
Попробуем найти какие нибудь закономерности и посмотрим можно ли как нибудь использовать
В скобках обозначим 2 последние цифры
1. 21^2019
21^1 = (21)
21^2 = 4(41)
21^3 = 92(61)
21^4 = 1944(81)
21^5 = 40841(01)
21^6 = 857661(21) ....
начались повторы последних двух цифр, то есть получается нам надо найти остатки от деления на 5 (период повтора 5)
2019 : 5 = 403 (ост 4)
Оканчивается также как 21^4 - это 81
2. 11^2020
аналогично
11^1 = (11)
11^2 = 1(21)
11^3 = 13(31)
11^4 = 146(41)
11^5 = 1610(51)
11^6 = 17715(61)
11^7 = 194871(71)
11^8 = 2143588(81)
11^9 = 23579476(91)
11^10 = 259374246(01)
11^11 = 2853116706(11)
цикл 10 значит надо найти остаток от деления степени на 10
2020 : 10 = 202 (остаток 0)
аналогично 11^10
две последние цифры 01

4 * 4.25 = 17