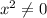, получим: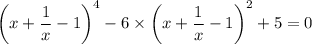
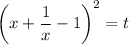, при условии что 
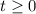, получим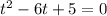
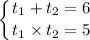
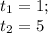
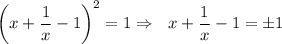
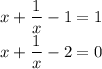
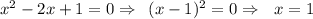
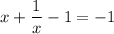
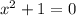
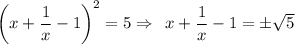
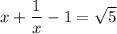
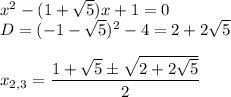
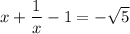
На столе лежало две пачки тетрадей, известно, что в одной из пачек тетрадей лежало в 2 раза больше. После того как из первой пачки убрали тетрадей, а во вторую добавили 29 тетрадей, то их количество стало одинаковым. Найти сколько было тетрадей во второй пачке изначально.
Пусть х - лежало изначально в первой пачке, тогда 2х - лежало во второй. По условию задачи после того как из первой стопки убрали 16 тетрадей, а во вторую добавили 29, то их количество стало одинаковым. Составим и решим уравнение:
2х - 16 = х + 29
2х - х = 29 + 16
х = 45
1) 45 (тетрадей) - было в первой пачке
2) 45 × 2 = 90 (тетрадей) - было во второй пачке
ответ: 90 тетрадей
1) х-у+х-у-2х-у=-3у
2) 0,2х-3-х+2-0,4х+1=-0,2х