Начнем рассуждать.
1) Если а=0, то уравнение х2+b=0 при b<0 имеет 2 корня, но они - разных знаков, при b=0 имеет 1 корень, при b>0 корней не имеет. Все эти условия нам не подходят. Значит, а отлично от нуля.
2) Далее, если a>0, то ось симметрии параболы у=x2 + ax + b будет находиться слева от оси Оу. Тогда один из возможных корней заведомо будет отрицательным. Нас это не устраивает. Значит, a<0.
3) Если b<0, то точка пересечения параболы у=x2 + ax + b с осью Оу будет находиться ниже нуля.Тогда опять один из возможных корней будет отрицательным. А если b=0, то график параболы у=x2 + ax + b проходит через (0; 0), т.е. корнем будет число 0. Нас и это не устраивает. Поэтому b>0.
3) Т.к. M (a;b) наудачу выбирается из квадрата с вершинами (–1; –1), (1; –1), (1; 1), (–1; 1), то ограничим а и b условиями: -1<a<0 и 0<b<1.
4) Далее для существования двух корней уравнения x2 + ax + b = 0 надо проверить, чтобы вершина параболы у=x2 + ax + b лежала ниже оси Ох.
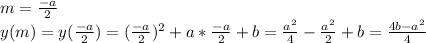
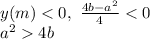
Последнее неравенство подтверждает то, что -1<a<0 и 0<b<1.
Два условия -1<a<0 и 0<b<1 описыват квадрат, площадь которого равна 1/4 площади квадрата с вершинами (–1; –1), (1; –1), (1; 1), (–1; 1). Значит, по правилу геометрической вероятности вероятность того, что корни уравнения x2 + ax + b = 0 окажутся действительными и положительными, равна 1/4.
последняя числа числа может быть
1 в квадрате 1
2- в квадрате 4
3 в квадрате 9
4 в квадрате 16
5 в квадрате 25
6 в квадрате 36
7 в квадрате 49
8 в квадрате 64
9 в квадрате 81
0 в квадрате 0
значит только 2 числа в квадрате имеют 1 на конце
значит 2/10=1/5=20%
последняя цифра числа может быть
1 в 4 степени 1
2 в 4 степени 16
3 в 4 степени 81
4 в 4 степени 256
5 в 4 степени 625
6 в 4 степени 1296
7 в 4 степени 2401
8 в 4 степени 4096
9 в 4 степени 6561
значит в 4х случаях на конце будет 1
значит 4/10=40%
Х= -0,578
2) -Х=-2ц1/4 * (-3/4)
-Х= - 1ц11/16
Х=1ц11/16
3) y= -3740 : (-5,5)
y= 680
4) -X= -0.009 : (-0,01)
-Х=0,9
Х= -0,9
5) -Х=9/28 : (-0,3)
-Х= -1ц1/14
Х=1ц1/14
6) -Х= -100 : (-3ц1/8)
-Х=32
Х= -32